Предмет: Геометрия,
автор: vladyes10
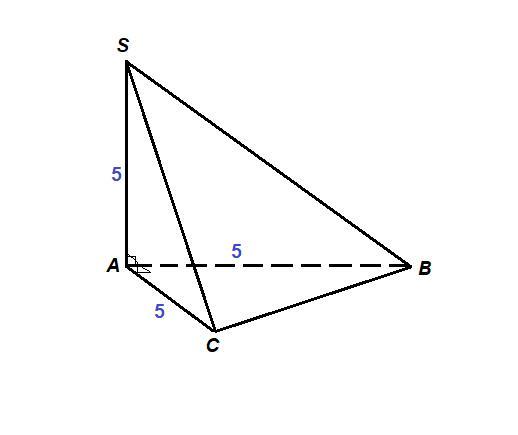
В тетраэдре SABC ∠SAB=∠SAC=∠BAC=90°. SA=AB=AC=5. Найди площадь грани SBC. (С чертежом).
Ответы
Автор ответа:
4
Ответ:
кв. ед.
Объяснение:
У треугольников SAB, SAC и BAC:
∠SAB = ∠SAC = ∠BAC = 90°,
SA = AB = AC,
значит ΔSAB = ΔSAC = ΔBAC по двум катетам, ⇒
SB = SC = BC = 5√2 как гипотенуза равнобедренного прямоугольного треугольника.
ΔSBC - равносторонний, его площадь:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: golodova91
Предмет: Химия,
автор: ivanovaanastas5
Предмет: Математика,
автор: Maльчuk
Предмет: Математика,
автор: suymaniga
Предмет: Обществознание,
автор: asdwsd