Предмет: Математика,
автор: bibaevrustam
Вычислить определенный интеграл методом подстановки
Приложения:
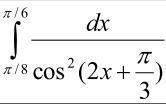
Ответы
Автор ответа:
1
Формулы, которые использовались в решение:
Решение:
Ответ: 1
Похожие вопросы
Предмет: Геометрия,
автор: nadyamoro2000
Предмет: Другие предметы,
автор: kairbek02
Предмет: Биология,
автор: dianadas
Предмет: Литература,
автор: алина5695
Предмет: Математика,
автор: rasulvanargiz9