Предмет: Математика,
автор: anonimmolly
пожалуйста, помогите решить
надо найти производные функции
Приложения:
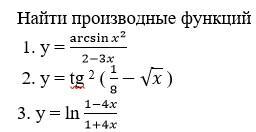
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Математика,
автор: Neznakomka08
Предмет: Русский язык,
автор: nire2653
Предмет: Литература,
автор: katabaharewa
Предмет: Математика,
автор: WordSnot
Предмет: Литература,
автор: grisinajana2003