Question

Помогите решить. Площади двух трапеций

Answer 1

Ответ:

Объяснение:

1)

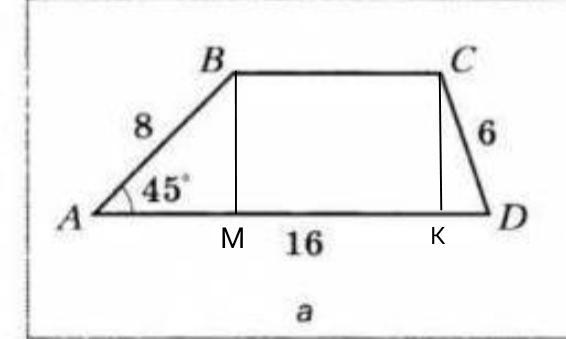
Рисунок а.

Проведём две высоты ВМ и СК.

ВМ=АМ, так как ∆АВМ- прямоугольный, равнобедренный

cos45°=AM/AB

√2/2=AM/8

AM=8√2/2=4√2 см.

ВМ=4√2 см.

СК=ВМ=4√2 см.

∆СКD- прямоугольный треугольник.

СD- гипотенуза.

СК и KD- катеты

По теореме Пифагора найдем

КD²=CD²-CK²=6²-(4√2)²=36-32=4см

КD=√4=2 см.

МК=AD-AM-KD=16-4√2-2=14-4√2 см.

МК=ВС=14-4√2см.

S(ABCD)=BM*(BC+AD)/2=4√2(16+14-4√2)/2=

=2√2(30-4√2)=60√2-16 см².

Ответ: 60√2-16см²

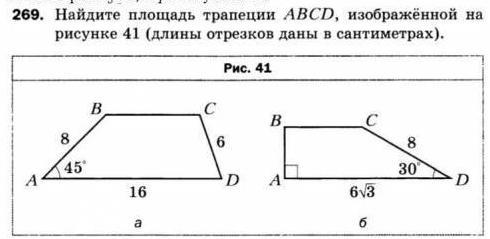
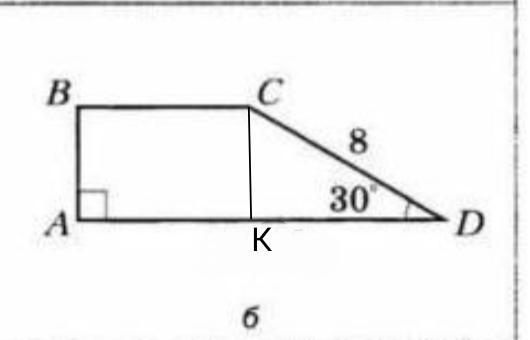
2) Рисунок б

Проведём высоту СК.

cos30°=KD/CD

√3/2=KD/8

KD=8√3/2=4√3 см

sin30°=CK/CD

1/2=CK/8

CK=8/2=4см высота трапеции.

BC=AD-KD=6√3-4√3=2√3 см.

S(ABCD)=CK(BC+AD)/2=4*(2√3+6√3)/2=

=2*8√3=16√3 см²

Ответ: 16√3см²