Question

30 БАЛЛОВ,СРОЧНО

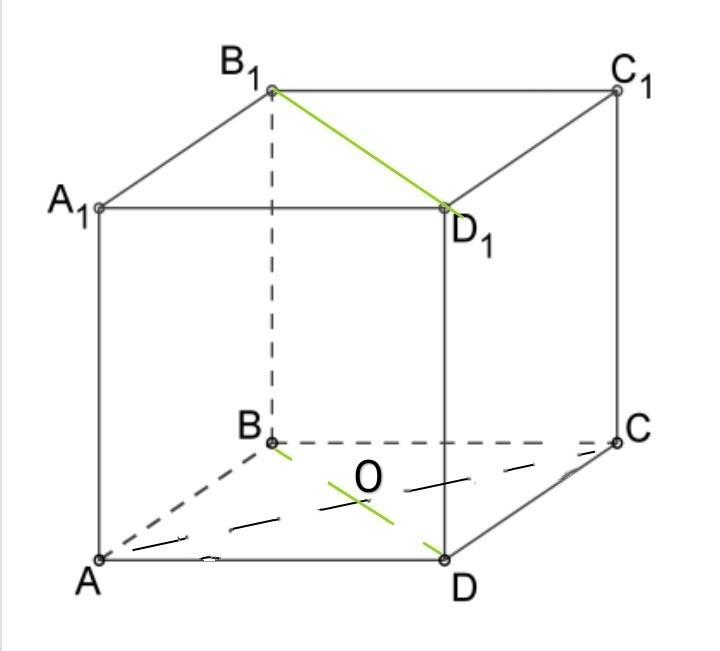
ABCDA1B1C1D1 — куб. Докажите, что прямая АС перпендикулярна к плоскости, которая проходит через точки B,B1,D1​

Answer 1

Объяснение:

1) Все грани куба являются квадратами.

По свойствам квадрата диагонали взаимно перпендикулярны. В нашем случае АС  ⟂ BD.

2) DD1 ⟂ DC по условию и DD1 ⟂ DA, DC ⋂ DA = D, тогда по признаку перпендикулярности прямой и плоскости DD1 ⟂ (ABC).

3) Так как DD1 ⟂ (ABC) , то она перпендикулярна любой прямой, лежащей в этой плоскости, в том числе DD1 ⟂ AC.

4) Получили, что

АС  ⟂ BD, AC ⟂ DD1, BD ⋂ DD1 = D, тогда по признаку  перпендикулярности прямой и плоскости АС ⟂ (ВВ1D1), что и требовалось доказать.