Question

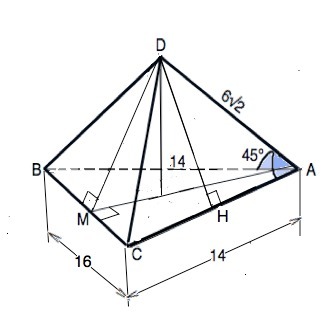
В тетраэдре  DABC ребро AD = 6 корней из 2, AB = AC =14 см, угол DAB = углу DAC = 45 градусов, BC = 16 см. Найдите площадь грани BDC 

Answer 1

Опустим из вершины тетраэдра D  высоту DН  на АС.

∆ АDН - прямоугольный, угол АDН=90°-45°=45°⇒

АН=DН=АD•sin45°=6

 СН=АС-АН=14-6=8

По т. Пифагора DС=√(DH²+СH²)=√(36+64)=10 см

∆ADB=∆ADC по двум сторонам и углу между ними⇒ BD=CD и

∆ BDC равнобедренный, высота DM   является его медианой,  ⇒   ВМ=СМ=16:2=8 см

DM делит ∆ BDC  на два равных  "египетских" треугольника с отношением сторон  DM:BM:BD=3:4:5. ⇒DM=6 (см). 

S ∆ BDC=DM•BC:2=6•16:2=48 см²