Question

Найди меньший катет прямоугольного треугольника, если гипотенуза равна 10 см, а катеты различаются в 0,75 раза

Answer 1

Ответ:

BC = 8 см

AB = 6 см

Объяснение:

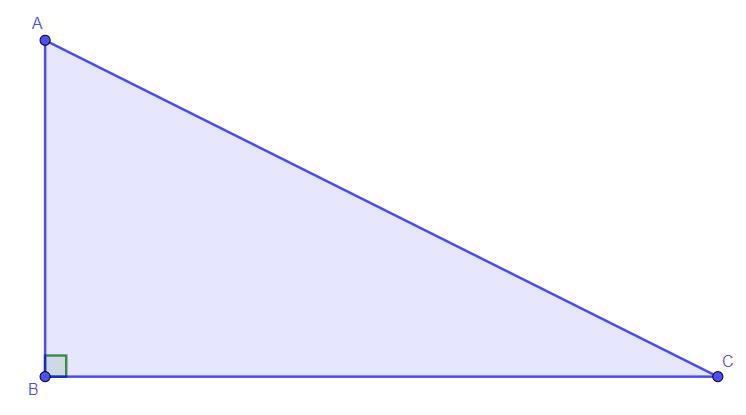
Дано: ∠ABC = 90°, $\dfrac{AB}{BC} = 0,75$ , AC = 10 см

Найти: AB,BC - ?

Решение: $\dfrac{AB}{BC} = 0,75 \Longrightarrow AB= 0,75BC$. Так как по условию угол

∠ABC = 90°, то по теореме Пифагора:

$AB^{2} + BC^{2} = AC^{2}$

$(0,75BC)^{2} + BC^{2} = 10^{2}$

$0,5625BC^{2} + BC^{2} = 100$

$1,5625BC^{2} = 100; BC > 0$ так как BC - сторона треугольника;

$\sqrt{1,5625BC^{2}} = \sqrt{100}$

$1,25BC = 10|:1,25$

$BC = 8$ см

$AB= 0,75BC = 0,75 \cdot 8 = 6$ см