Предмет: Алгебра,
автор: Azazeel
Решите неравенство log 3 (x-1)^2 / 9 * log 1/3 (x-1)/3 =
Приложения:
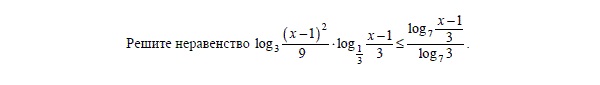
Ответы
Автор ответа:
4
ОДЗ x>1
2log(3) (x-1)/3*log(1/3) (x-1)/3-log(3) (x-1)/3≤0 (по формуле перехода к новому основанию)
log(3) (x-1)/3 (2log(1/3) (x-1)/3-1)≤0
нули неравенства
log (3) (x-1)/3=0 2log(1/3) (x-1)/3-1=0
x-1/3=1 x-1/3=1/√3
x=4 x=√3+1
при х=2 первый множитель отрицателен (=-1),а второй положителен (=1), значит знак произведения минус
при х=10 первый множитель положителен (=1), а второй отрицателен (=-3)
при х=3 первый множитель отрицателен и второй отрицателен
x∈(1;√3+1]V[4;+∞)
2log(3) (x-1)/3*log(1/3) (x-1)/3-log(3) (x-1)/3≤0 (по формуле перехода к новому основанию)
log(3) (x-1)/3 (2log(1/3) (x-1)/3-1)≤0
нули неравенства
log (3) (x-1)/3=0 2log(1/3) (x-1)/3-1=0
x-1/3=1 x-1/3=1/√3
x=4 x=√3+1
при х=2 первый множитель отрицателен (=-1),а второй положителен (=1), значит знак произведения минус
при х=10 первый множитель положителен (=1), а второй отрицателен (=-3)
при х=3 первый множитель отрицателен и второй отрицателен
x∈(1;√3+1]V[4;+∞)
Приложения:

Похожие вопросы
Предмет: Химия,
автор: EvgenySHEN
Предмет: Алгебра,
автор: mma0509
Предмет: Другие предметы,
автор: KZK24
Предмет: Окружающий мир,
автор: sally29
Предмет: Математика,
автор: hunterpol