Question

ПОМОГИИИИИИИИИТЕ 65 Баловввв

Answer 1

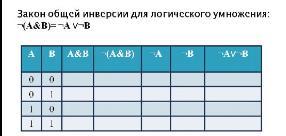
Левая часть:

$\begin{array}{|c|c|c|c|}A& B& A \mathop{\&} B& \lnot(A \mathop{\&} B)\\0& 0& 0& 1\\0& 1& 0& 1\\1& 0& 0& 1\\1& 1& 1& 0\end{array}$

A & B - логическое И. Как обычно, A & B = 1, если A = B = 1, а иначе 0.

$\lnot X$ - логическое НЕ, $\lnot 0=1$, $\lnot 1=0$.

Правая часть:

$\begin{array}{|c|c|c|c|c|}A&B&\lnot A&\lnot B&\lnot A\lor\lnot B\\0&0&1&1&1\\0&1&1&0&1\\1&0&0&1&1\\1&1&0&0&0\end{array}$

Здесь добавилось еще и логического ИЛИ: A ∨ B = 0, если A = B = 0, а иначе 1.

Таблицы истинности (последние столбцы) для левой и правой частей совпадают, закон доказан.

В виде одной таблицы:

$\begin{array}{|c|c|c|c|c|c|c|}A&B&A\mathop{\&}B&\lnot(A\mathop{\&}B)&\lnot A&\lnot B&\lnot A\lor\lnot B\\0&0&0&1&1&1&1\\0&1&0&1&1&0&1\\1&0&0&1&0&1&1\\1&1&1&0&0&0&0\end{array}$