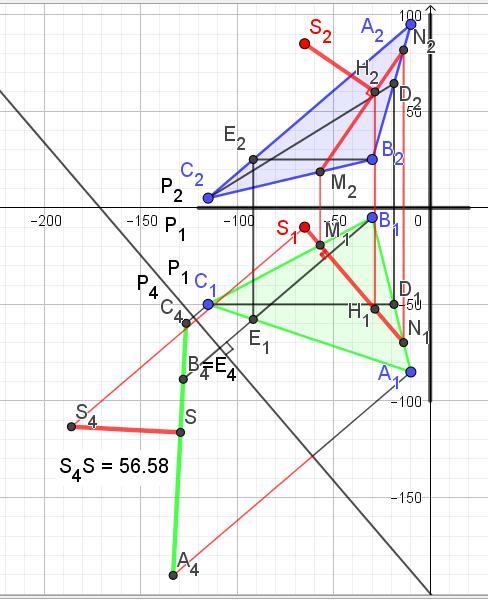
Определить кратчайшие расстояние от точки S до плоскости ABC
Ответы
Ход решения
Через вершину B треугольника ABC проводим фронталь и горизонталь.
Переводим ABC в проецирующее положение. Для этого перпендикулярно В1Е1 вводим новую фронтальную плоскость Р4. Проецируем на неё точку S и треугольник ABC.
Из точки S4 проводим перпендикуляр к А4С4.
Длина отрезкаS4S – искомое расстояние между плоскостью треугольника ABC и точкой S.
Если требуется аналитическая проверка найденного расстояния, то по координатам точек А, В и С находим уравнение плоскости АВС:
95x -111y +154z - 6145 = 0.
Затем находим расстояние от точки S до плоскости АВС.
Для вычисления расстояния от точки S(Sx; Sy; Sz) до плоскости Ax + By + Cz + D = 0 используем формулу:
d = |A·Mx + B·My + C·Mz + D| /√(A² + B² + C²)
Подставим в формулу данные:
d = |95·65 + (-111)·10 + 154·85 + (-6145)| √(95² + (-111)² + 154²) = |6175 - 1110 + 13090 - 6145| /√(9025 + 12321 + 23716) =
= 12010 /√45062 = 6005√45062 /22531 ≈ 56.57672.
Полученное расчётное значение полностью совпадает с графическим расчётом.