Question

Решение квадратных уравнений. Урок 3 Установи соответствие между квадратным уравнением и его корнями.

Answer 1

Объяснение:

$x^{2} -3x-4=0;\\D= (-3) ^{2} -4\cdot1\cdot(-4)=9+16=25=5^{2} \\\\x{_1}= \dfrac{3-5}{2} =\dfrac{-2}{2} =-1;\\\\x{_2}= \dfrac{3+5}{2} =\dfrac{8}{2} =4.$

Ответ: - 1; 4.

$x^{2} +3x-4=0;\\D= 3 ^{2} -4\cdot1\cdot(-4)=9+16=25=5^{2} \\\\x{_1}= \dfrac{-3-5}{2} =\dfrac{-8}{2} =-4;\\\\x{_2}= \dfrac{-3+5}{2} =\dfrac{2}{2} =1.$

Ответ: - 4; 1.

$x^{2} +5x+4=0;\\D= 5 ^{2} -4\cdot1\cdot4=25-16=9=3^{2} \\\\x{_1}= \dfrac{-5-3}{2} =\dfrac{-8}{2} =-4;\\\\x{_2}= \dfrac{-5+3}{2} =\dfrac{-2}{2} =-1.$

Ответ: - 4; - 1.

$x^{2} -5x+4=0;\\D=(- 5) ^{2} -4\cdot1\cdot4=25-16=9=3^{2} \\\\x{_1}= \dfrac{5-3}{2} =\dfrac{2}{2} =1;\\\\x{_2}= \dfrac{5+3}{2} =\dfrac{8}{2} =4.$

Ответ : 1; 4.

Answer 2

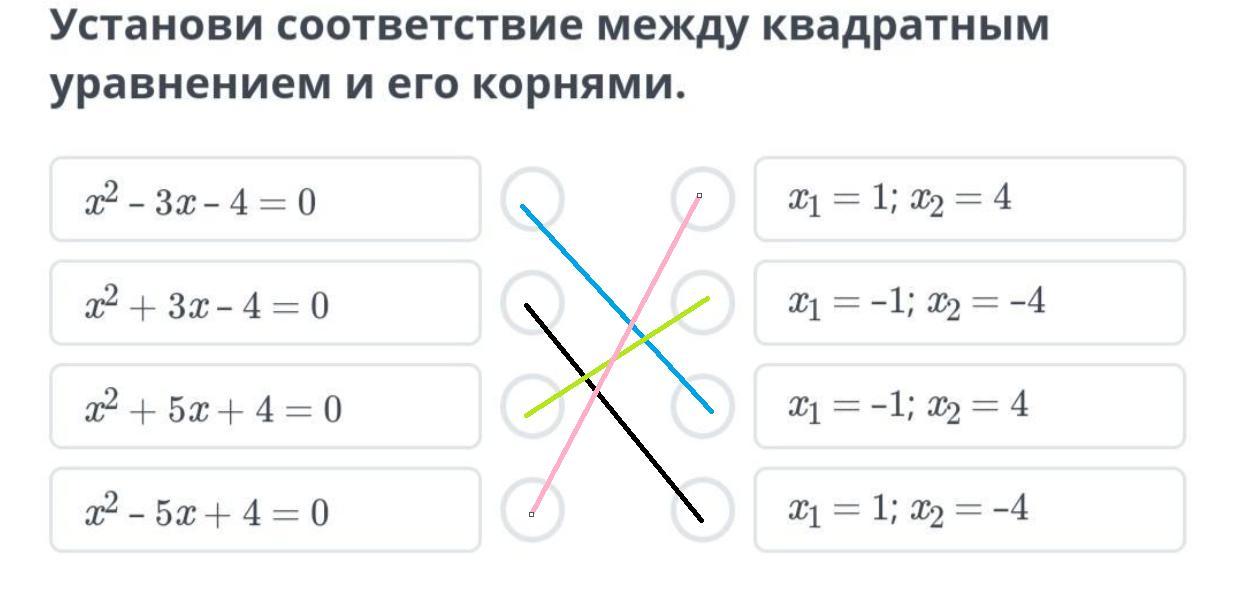
Ответ и Объяснение:

Квадратное уравнение a·x²+b·x+c = 0 имеет корни

x₁ = (-b-√D)/(2·a) и x₂ = (-b+√D)/(2·a),

если D = b²-4·a·c > 0.

Решение.  

Для квадратного уравнения x²-3·x-4 = 0 коэффициенты равны:

a = 1, b = -3, c = -4.

Тогда

D = (-3)²-4·1·(-4) = 9+16 = 25 = 5² >0, то есть √D = 5:

x₁ = (-(-3)-5)/(2·1) = (3-5)/2 = -2/2 = -1;

x₂ = (-(-3)+5)/(2·1) = (3+5)/2 = 8/2 = 4.

Корни: x₁ = -1; x₂ = 4.

Для квадратного уравнения x²+3·x-4 = 0 коэффициенты равны:

a = 1, b = 3, c = -4.

Тогда

D = 3²-4·1·(-4) = 9+16 = 25 = 5² >0, то есть √D = 5:

x₁ = (-3-5)/(2·1) = -8/2 = -4;

x₂ = (-3+5)/(2·1) = 2/2 = 1.

Корни: x₁ = -4; x₂ = 1.

Для квадратного уравнения x²+5·x+4 = 0 коэффициенты равны:

a = 1, b = 5, c = 4.

Тогда

D = 5²-4·1·4 = 25-16 = 9 = 3² >0, то есть √D = 3:

x₁ = (-5-3)/(2·1) = -8/2 = -4;

x₂ = (-5+3)/(2·1) = -2/2 = -1.

Корни: x₁ = -4; x₂ = -1.

Для квадратного уравнения x²-5·x+4 = 0 коэффициенты равны:

a = 1, b = -5, c = 4.

Тогда

D = (-5)²-4·1·4 = 25-16 = 9 = 3² >0, то есть √D = 3:

x₁ = (-(-5)-3)/(2·1) = (5-3)/2 = 2/2 = 1;

x₂ = (-(-5)+3)/(2·1) = (5+3)/2 = 8/2 = 4.

Корни: x₁ = 1; x₂ = 4.