Предмет: Алгебра,
автор: sevaranorova136
помогите пожалуйста разобраться с примером
Приложения:
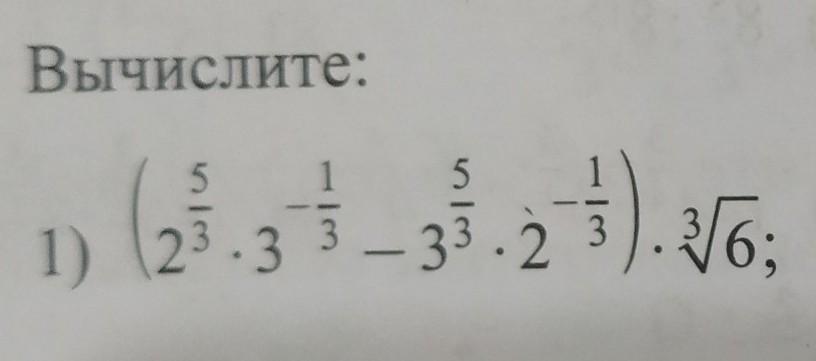
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Выражаем с положительным показателем, используя :
Вычисляем произведение:
Распределяем через скобки:
Используя , преобразовываем выражения:
Произведение корней одинаковой степени равно корню произведения:
Упрощаем корни:
Вычисляем степени:
Умножаем числа:
Упрощаем корни:
Сокращаем дроби на и
:
Вычитаем числа:
sevaranorova136:
огромное спасибо
Похожие вопросы
Предмет: Физика,
автор: motolyga2002
Предмет: Українська мова,
автор: 24674382
Предмет: Русский язык,
автор: Jennu
Предмет: Физика,
автор: Sergio27