Предмет: Геометрия,
автор: mirkamirka1201own65c
90. Знайти площу бічної поверхні правильної чотирикут-
ної піраміди, бічне ребро якої дорівнює 8 см, а висо-
4 см.
та
Приложения:

Ответы
Автор ответа:
1
Ответ:
32√15 см²
Объяснение:
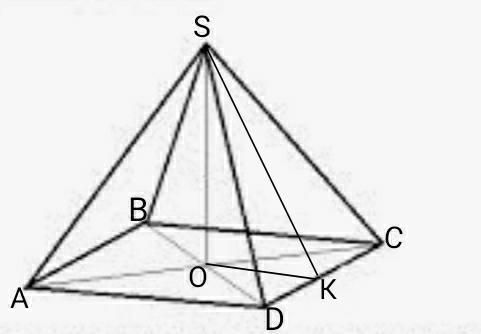
SABCD- пирамида
ABCD- квадрат.
SC=SA=SB=SD=8см
SO=4см
Sбок.=?
Решение.
∆SOC - прямоугольный.
SO и ОС - катеты
SC- гипотенуза.
По теореме Пифагора найдем катет
ОС²=SC²-SO²=8²+4²=64-16=48
OC=√48=4√3 см. половина диагонали.
АС=2*ОС=2*4√3=8√3 см
Сторона квадрата
ВС=АС/√2=8√3/√2=4√6 см сторона квадрата.
РАВСD=4*BC=4*4√6=16√6 см периметр квадрата.
ОК=1/2*BC=4√6:2=2√6 см проекция апофемы на плоскость (АВС)
∆SOK - прямоугольный.
По теореме Пифагора
SK²=SO²+OK² =4²+(2√6)²=16+24=40 см
SK=√40=2√10 см.
Sбок=PABCD*SK/2=16√6*2√10/2=32√60/2=32*2√15/2=32√15 см² площадь боковой поверхности пирамиды
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Alena24567890
Предмет: Геометрия,
автор: mamafaza
Предмет: Математика,
автор: ОЛЬГА786
Предмет: Физика,
автор: lerabrusenskaya