Question

решите квадратные неравенства 3 x квадрате минус 5 Икс плюс 2 больше или равно нулю​

Answer 1

3x² - 5x + 2 ≥ 0.

Рассмотрим квадратичную функцию у = 3x² - 5x + 2 и выясним, где эта функция принимает неотрицательные значения, т.е. у ≥ 0. Найдем нули функции:

3x² - 5x + 2 = 0,

D = 25 - 4 · 2 · 3 = 25 - 24 = 1; √1 = 1;

x₁ = (5 - 1)/(2 · 3) = 4/6 = 2/3,

x₂ = (5 + 1)/(2 · 3) = 6/6 = 1.

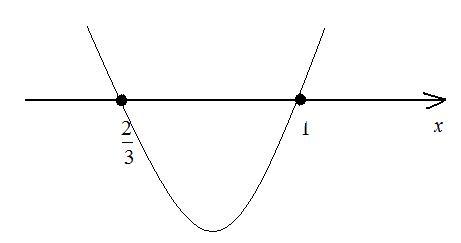
Построим схематически график функции у = 3х² - 5x + 2 (см. рисунок.)

Значит, у ≥ 0, если x є (-∞; 2/3] ∪ [1; +∞).

Ответ: (-∞; 2/3] ∪ [1; +∞).