Предмет: Геометрия,
автор: Angelina180799
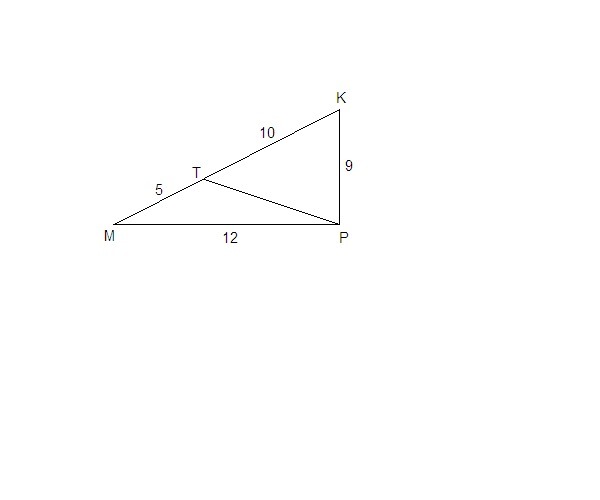
На стороне MK треугольника MKP отмечена точка T так, что MT = 5см, KT = 10 см. Найдите площади треугольников MPT и KPT, если MP = 12 см, KP = 9 см.
Ответы
Автор ответа:
0
15² = 9² + 12²
225 = 81 + 144
225 = 225
Треугольник МКР прямоугольный по теореме, обратной теореме Пифагора.
Большая сторона МК - гипотенуза, значит, угол Р равен 90°.
Smkp = (МР ·РК)/2 = (12 · 9)/2 = 54 см²
Треугольники МРТ и КРТ имеют общую высоту, проведенную из вершины Р. Тогда их площади относятся как стороны, к которым проведена общая высота.
Smpt : Skpt = MT : TK = 5 : 10 = 1 : 2
Smpt = Smpk/3 = 54/3 = 18 см²
Skpt = 2Smpk/3 = 2 · 54/3 = 36 см²
225 = 81 + 144
225 = 225
Треугольник МКР прямоугольный по теореме, обратной теореме Пифагора.
Большая сторона МК - гипотенуза, значит, угол Р равен 90°.
Smkp = (МР ·РК)/2 = (12 · 9)/2 = 54 см²
Треугольники МРТ и КРТ имеют общую высоту, проведенную из вершины Р. Тогда их площади относятся как стороны, к которым проведена общая высота.
Smpt : Skpt = MT : TK = 5 : 10 = 1 : 2
Smpt = Smpk/3 = 54/3 = 18 см²
Skpt = 2Smpk/3 = 2 · 54/3 = 36 см²
Приложения:
Похожие вопросы
Предмет: Математика,
автор: bruururbubrndibruxbr
Предмет: Окружающий мир,
автор: bisenbaevaajgul
Предмет: Английский язык,
автор: davletiarbekzat
Предмет: Алгебра,
автор: Anastasiyamu
Предмет: Биология,
автор: makeup