Предмет: Геометрия,
автор: EMINEM376
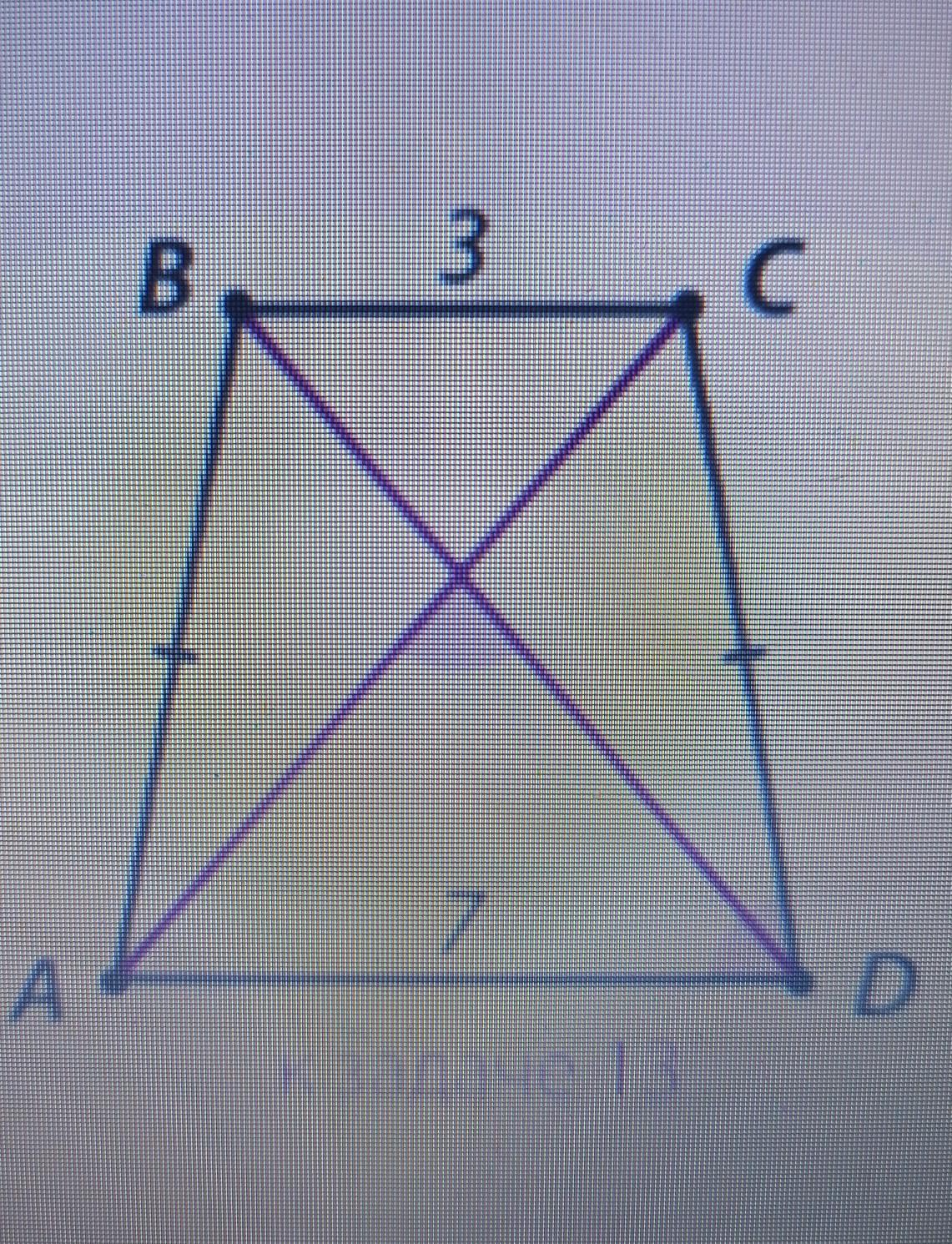
отмеченный на рисунке острый угол равнобокой трапеции равен углу между ее диагоналями. найдите периметр этой трапеции, если ее основания равны 3 и 7
Приложения:
Ответы
Автор ответа:
8
Ответ:
24 ед.
Объяснение:
Дано: АВСD - равнобедренная трапеция.
ВС=3; АD=7;
∠1=∠D
Найти: Р (АВСD)
Решение:
1. Рассмотрим ΔАВС и ВСD.
АВ=СD (АВСD - равнобедренная трапеция)
ВС - общая
В равнобедренной трапеции диагонали равны.
⇒ BD=AC
⇒ ΔАВС = ВСD (по 3-му признаку)
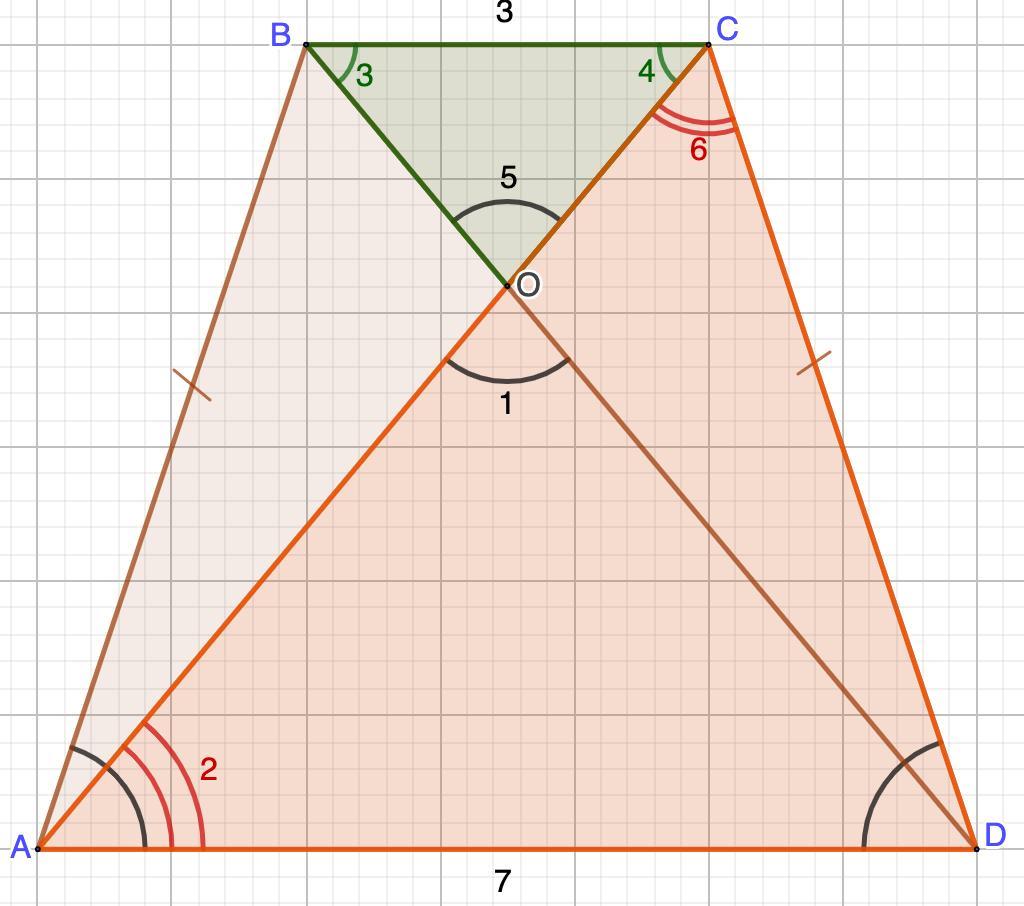
∠3=∠4 (как соответственные элементы)
2. ∠5=∠1 - вертикальные.
⇒ ∠D=∠5=∠1
∠2=∠4 - накрест лежащие при ВС || AD и секущей АС.
3. Рассмотрим ΔВОС и ΔАСD
∠2=∠4 (п.2)
∠D=∠5 (п.2)
⇒ ΔВОС ~ ΔАСD (по 1 признаку)
⇒ ∠6=∠3
Выпишем все равные углы:
∠6=∠3=∠4=∠2
⇒ ΔАСD - равнобедренный (углы при основании равны)
⇒ AD=DC=7
4. АВ=СD=7
Периметр - сумма длин всех сторон трапеции.
Р (АВСD) = 3+7+7+7=24
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: artemkanado
Предмет: Русский язык,
автор: ahmetzhanovada
Предмет: Русский язык,
автор: ain23a
Предмет: Математика,
автор: vypukina
Предмет: Математика,
автор: Juliana07Koshkina