Предмет: Алгебра,
автор: bapataidamir2004
Найдите х. Нужна помощь!!!!!!
Приложения:
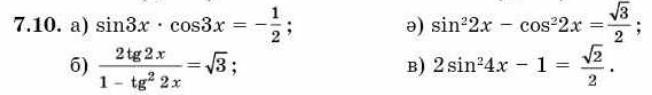
Ответы
Автор ответа:
1
bapataidamir2004:
Спасибо огромное! Если не трудно можете помочь с этой задачей. https://znanija.com/task/39753567
Похожие вопросы
Предмет: Английский язык,
автор: saleswoman
Предмет: Русский язык,
автор: лучик2006
Предмет: Английский язык,
автор: grad7316
Предмет: География,
автор: Амерланиша
Предмет: Алгебра,
автор: RIP11111