Предмет: Геометрия,
автор: kotdikaprio
Знайти радіус описаного кола навколо рівнобічної трапеції, якщо основи 7 см та 23, а бічна—17 см.
Ответы
Автор ответа:
0
Ответ: 8,5√2 см.
Объяснение:
"Найти радиус описанного круга вокруг равнобедренной трапеции, если основания 7 см и 23, а боковая—17 см."
***
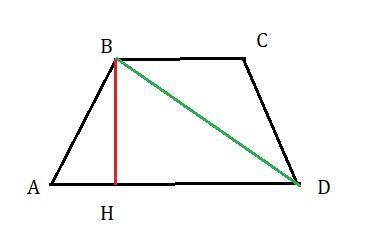
ABCD - трапеция. Проведем ВН -высоту трапеции.
Радиус описанной около трапеции окружности можно найти по формуле:
R=BD/2SinA, где BD - диагональ трапеции.
SinA=BH/AB.
BH=AB²-AH²;
AH=(23-7)/2=8 см.
ВН=√17²-8²=√289-64=√225=15 см.
Диагональ BD=√BH²+DH²=√15²+(23-8)²=√225+225=15√2 см.
SinA=BH/AB=15/17;
R=15√2/2*(15/17)=8,5√2 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: AnyaKrip
Предмет: Русский язык,
автор: Ieo
Предмет: Другие предметы,
автор: polina031410
Предмет: Математика,
автор: VALERIKSAIFYLL