Предмет: Геометрия,
автор: nikolpinchuk00
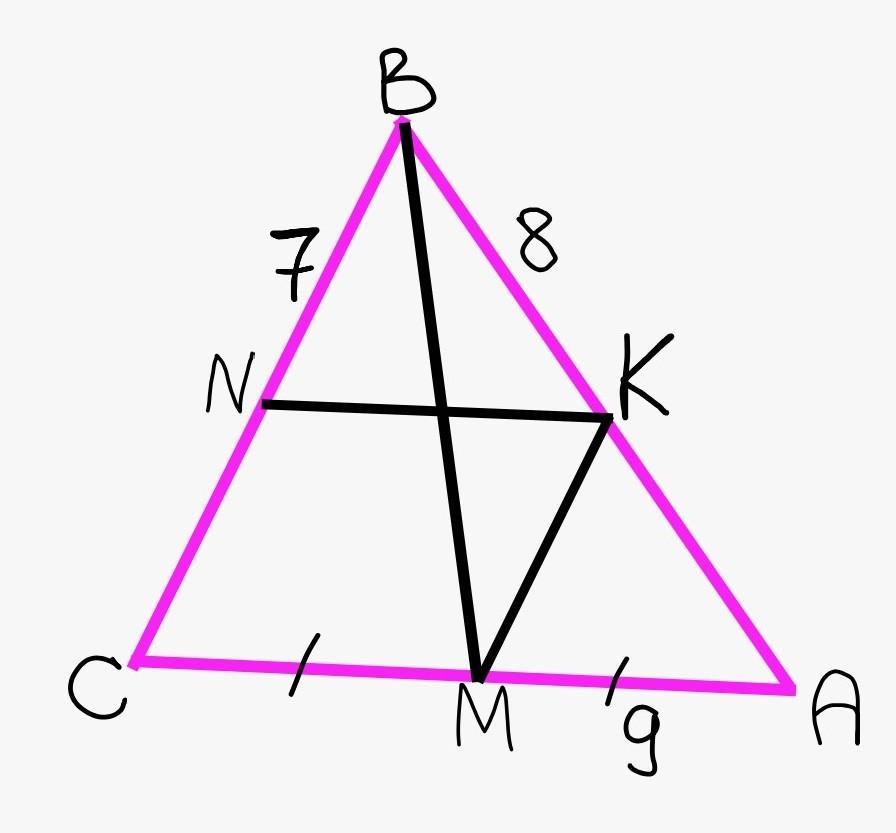
в треугольнике ABC проведена медиана BM, отрезки МК||BC (K принадлежит АВ), KN||АС (N принадлежит ВС). Найдите периметр четырехугольника AKNC, если КВ= 8 см, АМ=9 см, ВN= 7 см
Ответы
Автор ответа:
2
Ответ:
Так как точка ВМ – медиана, то точка М – середина стороны АС и СМ=АМ=9 см, тогда АС=СМ+АМ=9+9=18 см;
МК//ВС по условию;
Тогда МК – средняя линия ∆АВС, так как проходит через середину одной из сторон треугольника и параллелен другой.
Исходя из этого: АК=ВК=8 см.
Тогда точка К – середина АВ.
NK//AC по условию
Следовательно NK – средняя линия ∆АВС, так как проходит через середину одной из сторон треугольника и параллелен другой.
Следовательно CN=BN=7 см, NK=0,5*AC=0,5*18=9 см.
P(AKNC)=AK+KN+NC+AC=8+9+7+18=42 см.
Ответ: 42 см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: arihon2004
Предмет: Английский язык,
автор: BEATSPILL
Предмет: Английский язык,
автор: alina0709eys
Предмет: История,
автор: 238football
Предмет: История,
автор: Особенности