Предмет: Математика,
автор: nikita161698
помогите решить двойной интеграл
Приложения:
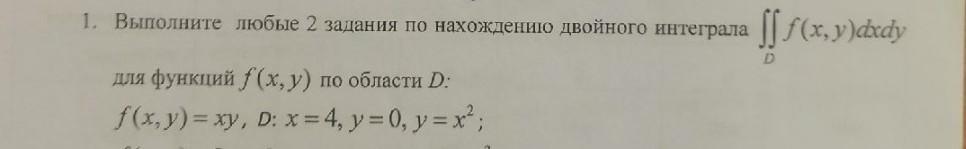
Ответы
Автор ответа:
1
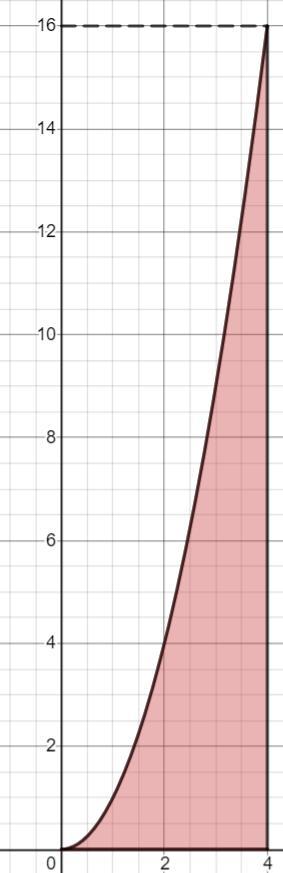
Для области D определим границы (см. график)
Таким образом, двойной интеграл разобьется на повторный: сначала по y (границы зависят от x), затем по x . Также можем разделить переменные в подынтегральной функции.
Приложения:
nikita161698:
спасибо огромное что выручил
Похожие вопросы
Предмет: Английский язык,
автор: mardim123456
Предмет: Українська мова,
автор: mariadiakevich
Предмет: Русский язык,
автор: nataljasemiono
Предмет: Математика,
автор: monguszamian
Предмет: Физика,
автор: Аноним