Question

1 напишите уравнение окружности с центром в точке (-2;3) и радиусом R=3

2.найдите множество точек координатной плоскости, которое задано системой неравенств:
${x}^{2} + {y}^{2} \leqslant 25 \\ y \geqslant 0$
помогите прошу срочно надо
​

Answer 1

Ответ:

1. (x+2)²+(y-3)²=9

2. хє[-5;5]

ує[0;5]

Объяснение:

1. Уравнение окружности: (x-a)²+(y-b)²=r²

(x-(-2))²+(y-3)²=3²

(x+2)²+(y-3)²=9.

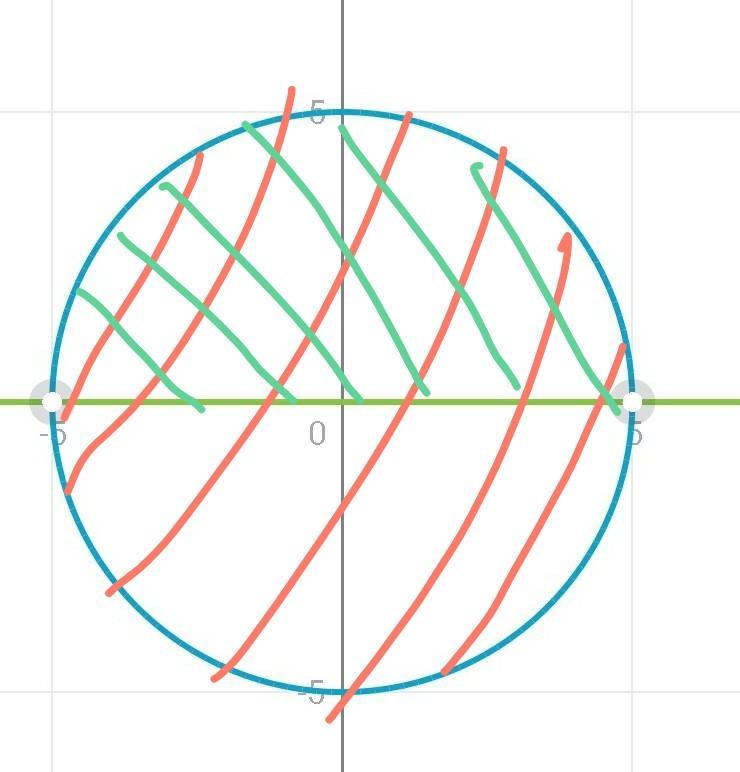
2. Построим окружность с центром (0;0) и радиусом 5 для х²+у²=25, следовательно хє[-5;5]

В этой же координатной плоскости по Оси Ох проведем луч у=0.

т.к у≥0 yє[0;5]

Ответ: хє[-5;5]

ує[0;5]

Показал на рисунке где 2 полосы это подходящее.