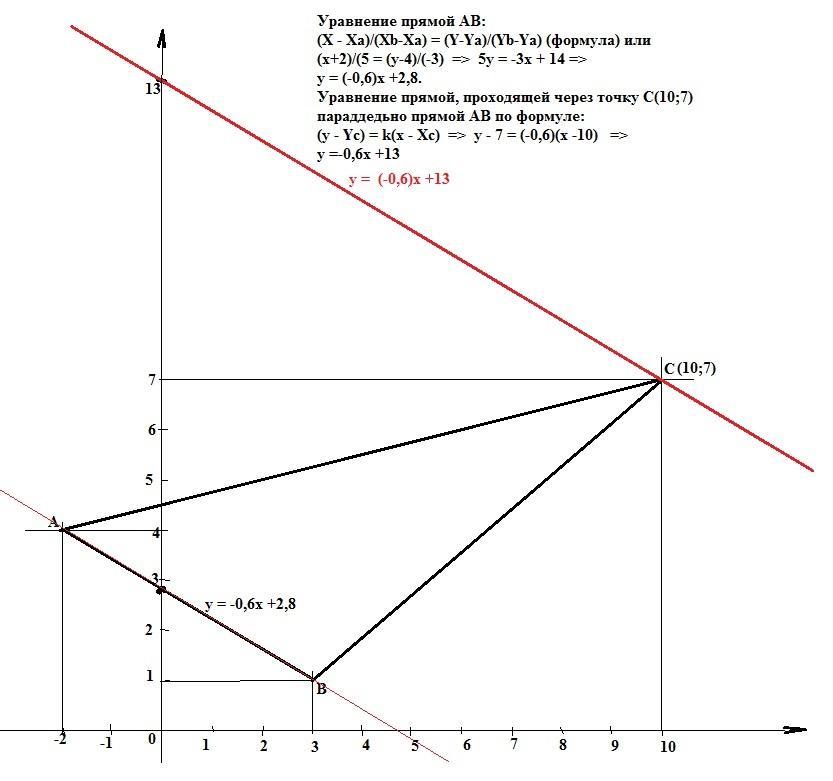
даны вершины Триугольника АВС: А(-2,4), В(3,1), С(10,7) Найти: а) уравнение прямой проходящей через вершину С параллельно стороне АВ; б) расстояние от точки С до прямой АВ.
Ответы
Ответ:
а) y =-0,6x +13
б) 51/√34 ≈ 8,75 ед.
Объяснение:
а). Уравнение прямой АВ:
(X - Xa)/(Xb-Xa) = (Y-Ya)/(Yb-Ya) (формула) =>
(x+2)/(5 = (y-4)/(-3) => 5y = -3x + 14 =>
y = (-0,6)x +2,8.
Уравнение прямой, проходящей через точку С(10;7) параллельно прямой АВ по формуле:
(y - Yc) = k(x - Xc) => y - 7 = (-0,6)(x -10) =>
y =-0,6x +13
б). Расстояние от точки М(Xm;Ym) до прямой Ax +By +C = 0 находится по формуле:
d = (A·Xm + B·Ym +C)/√(A²+B²).
В нашем случае уравнение прямой АВ: 3x + 5y - 14 =0.
Точка С(10:7). Тогда расстояние равно:
d = (3·10 +5·7 + (-14)/√(3²+5²) = 51/√34 ≈ 51/5,83 ≈ 8,75 ед.
Или так:
Площадь треугольника АВС, заданного координатами его вершин найдем по формуле:
S=(1/2)[(X1-X3)(Y2-Y3)-(X2-X3)(Y1-Y3)]. =>
S = (1/2)[(-2-10)(1-7)-(3-10)(4-7)] = 51/2 = 25,5.
Тогда высота СН к стороне АВ при модуле АВ, равном |AB| = √(5²+(-3)²) = √34:
СН = 2S/AB = 51/√34 ≈ 51/5,83 ≈ 8,75 ед.