Question

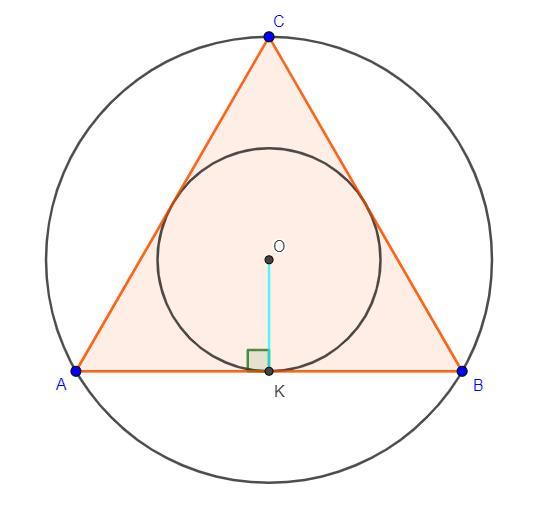
Треугольник ABC-равносторонний. Радиус OK вписанной окружности равен корень из 3 см. Найдите длину стороны AB

Answer 1

Ответ:

6 см

Объяснение:

Дано: AB = BC = AC, OK = $\sqrt{3}$ см, OK - радиус вписанной окружности

Найти: AB - ?

Решение: Так как по условию треугольник ΔABC - равносторонний, то по свойствам равностороннего треугольника его центр вписанной и описанной окружности совпадают, то есть точка O - цент вписанной и описанной окружности. По свойствам равностороннего треугольника все его углы равны 60° .Пусть R - радиус описанной окружности для треугольника ΔABC.По формуле Эйлера: $d^{2} = R^{2} - 2R*OK$, где d - расстояние между центрами вписанной и описанной окружностей. Так как их центры совпадают, то $d = 0$, тогда $0 = R^{2} - 2R * OK$.

$2R * OK = R^{2} |:R$

$R = 2OK = 2\sqrt{3}$ см.

По следствию из теоремы синусов для треугольника ΔABC:

$R = \dfrac{AB}{2 \sin \angle ACB} \Longrightarrow AB = 2R * \sin \angle ACB = 2 * 2\sqrt{3} * \sin 60^{\circ} = 4\sqrt{3} * \dfrac{\sqrt{3} }{2} =$

$= 2 * 3 = 6$ см.