Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста упростить тригонометрическое выражение.Срочно
Приложения:
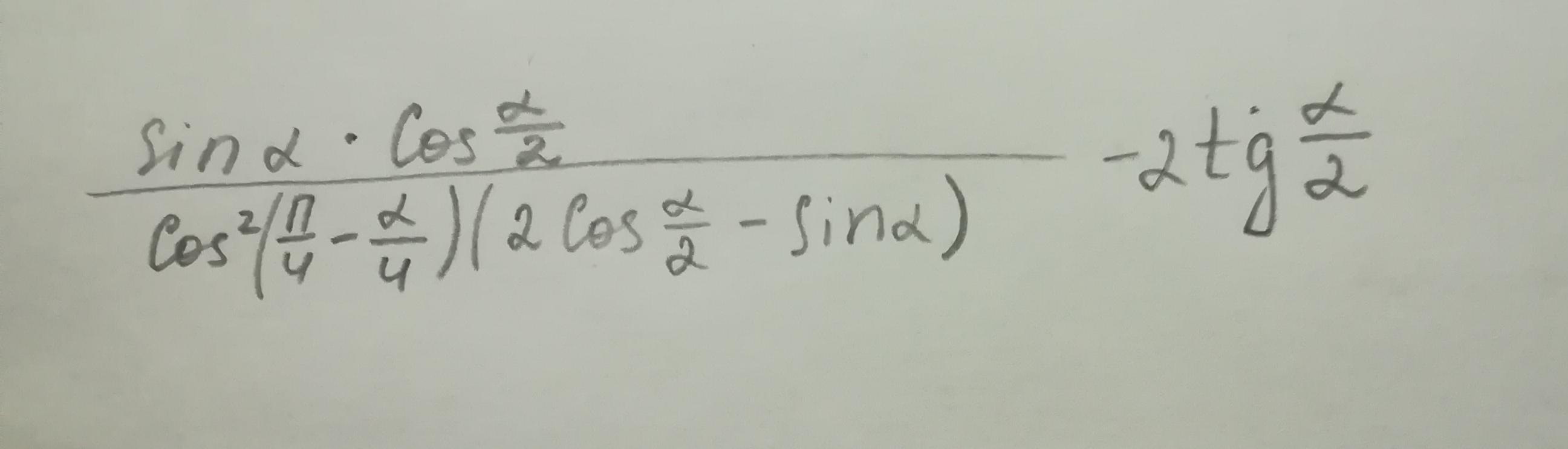
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: zalinababazhan
Предмет: Русский язык,
автор: potahica
Предмет: Русский язык,
автор: 5566775676545554
Предмет: Геометрия,
автор: Раадша