Предмет: Математика,
автор: Bes1lo
Без Лопиталя как решать?
Приложения:
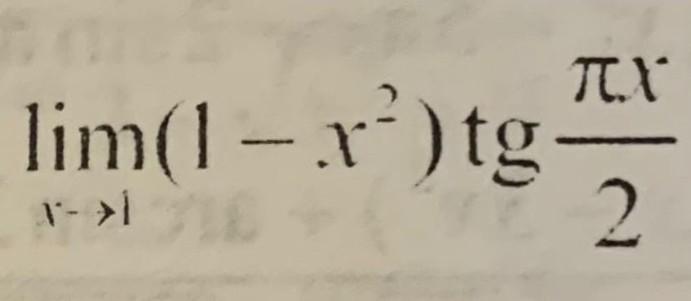
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: innagolden
Предмет: Другие предметы,
автор: насих11
Предмет: Русский язык,
автор: ajratik
Предмет: Физика,
автор: SidykinaNadegda1
Предмет: География,
автор: Mari22568