Предмет: Математика,
автор: TheBuktor
СРОЧНО! 50 БАЛЛОВ
Постройте на координатной плоскости xOy множество точек, удовлетворяющих заданным соотношениям
1. 
2. 
3. 
4.
Объясните принцип, как решить
TheBuktor:
Разобрался. Оказывается, нужно начертить графики для крайних границ (границы) множества, например, в первом примере будет x + y = 0 и 2x - y = 0, потом выделить части, подходящие под решение каждой функции из 1 примера, и найти общую часть.
Ответы
Автор ответа:
0
Ответ:
решается так
Пошаговое объяснение:
у - |х - 3| + 1 = 0
у = |х - 3| - 1 -- это модульная функция, которая смещена на 3 вправо и на 1 вниз.
Найдем некоторые точки функции:
x = 3, y = -1
x = 2, y = 0
x = 4, y = 0
Приложения:
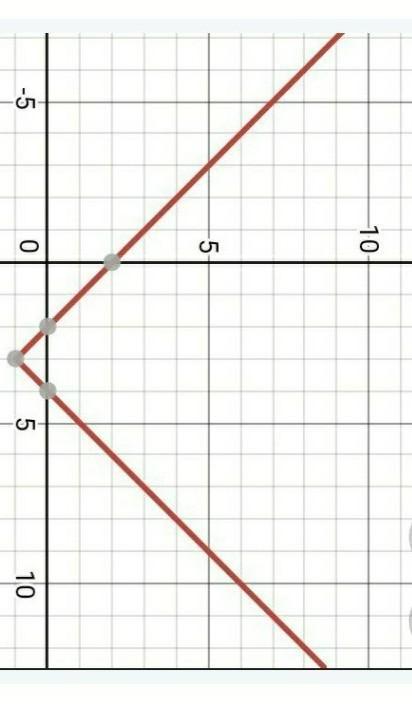
это образец
А системой модешь объяснить? Просят множество точек, а не график функции, и как быть, если в функции не x + y = 0, а x + y ⩾ 0?
Похожие вопросы
Предмет: Другие предметы,
автор: насих11
Предмет: Русский язык,
автор: ajratik
Предмет: Русский язык,
автор: Irinaanohina70
Предмет: География,
автор: Mari22568
Предмет: Математика,
автор: shatalova80