Question

Задание: Найдите радиус окружности, описанной около равнобедренного треугольника с основанием 12 см и боковой стороной 10 см. ​

Answer 1

Ответ:

R= 6,25 см.

Объяснение:

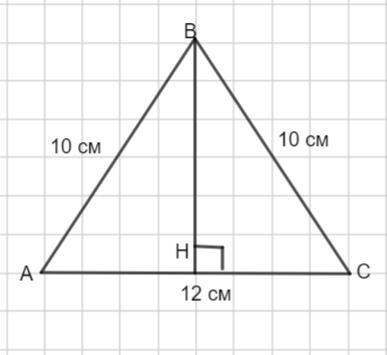
Рассмотрим Δ АВС - равнобедренный.

АВ=ВС =10 см, АС= 12 см.

1 способ.

Проведем высоту  ВН. В равнобедренном треугольнике высота проведенная к основанию является медианой .

Тогда АН= НС= 12:2=6 см.

Рассмотрим прямоугольный треугольник АВН. Найдем высоту ВН по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

$AB^{2} =AH^{2} +BH^{2} ;\\BH^{2}=AB^{2} -AH^{2};\\BH=\sqrt{AB^{2} -AH^{2}} ;\\BH=\sqrt{10^{2} -6^{2} } =\sqrt{100-36} =\sqrt{64} =8$

BH= 8 см.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

$sinA=\dfrac{BH}{AB} \\\\sinA=\dfrac{8}{10} =0,8$

Радиус окружности описанной около треугольника определяется по формуле

$R= \dfrac{a}{2sin\alpha } ;\\\\R=\dfrac{BC}{2sinA} ;\\\\R=\dfrac{10}{2\cdot0,8}=\dfrac{100}{16}=\dfrac{25}{4}=6\dfrac{1}{4}=6,25$

R= 6,25 см.

2 способ

Радиус окружности описанной около треугольника определяется по формуле

$R=\dfrac{abc}{4S}$

Найдем площадь треугольника

$S= \dfrac{1}{2} \cdot AC\cdot BH;\\S= \dfrac{1}{2} \cdot 12\cdot 8=6\cdot8= 48$

S= 48 см².

Тогда

$R= \dfrac{10\cdot10\cdot12}{4\cdot48} =\dfrac{100}{16} =\dfrac{25}{4} =6\dfrac{1}{4} =6,25$