Предмет: Алгебра,
автор: shortercartlee
Помогите решить пожалуйста!! Нужно решить по действиям
Пример:тождество
1 действие
2 действие
3 если естт
Приложения:
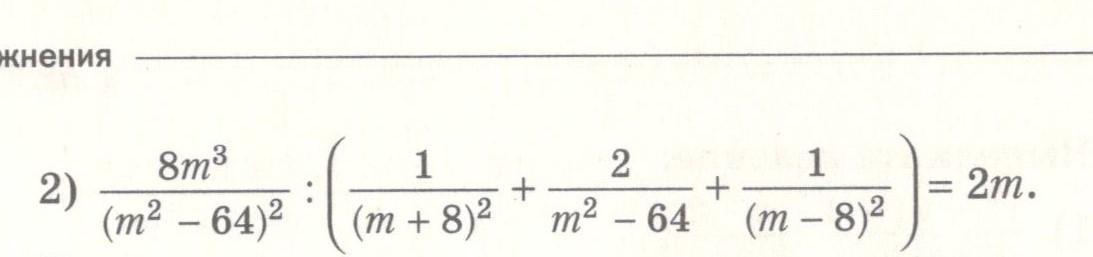
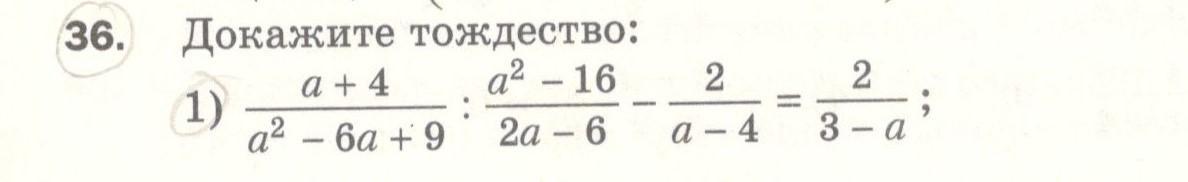
Ответы
Автор ответа:
0
Объяснение:
Преобразуем левую часть .
Выполним действия в скобках
Выполним деление дробей.
Левая часть равна правой части и тождество доказано.
№36
Преобразуем левую часть
Выполним деление дробей
Выполним вычитание
Левая часть равна правой части и тождество доказано.
Похожие вопросы
Предмет: Русский язык,
автор: KpacuBbIu
Предмет: Английский язык,
автор: Евстиграфия
Предмет: Другие предметы,
автор: Vladik1232
Предмет: Алгебра,
автор: ololoshLee
Предмет: Алгебра,
автор: ololoshLee