бред писать не нужно!!!
Ответы
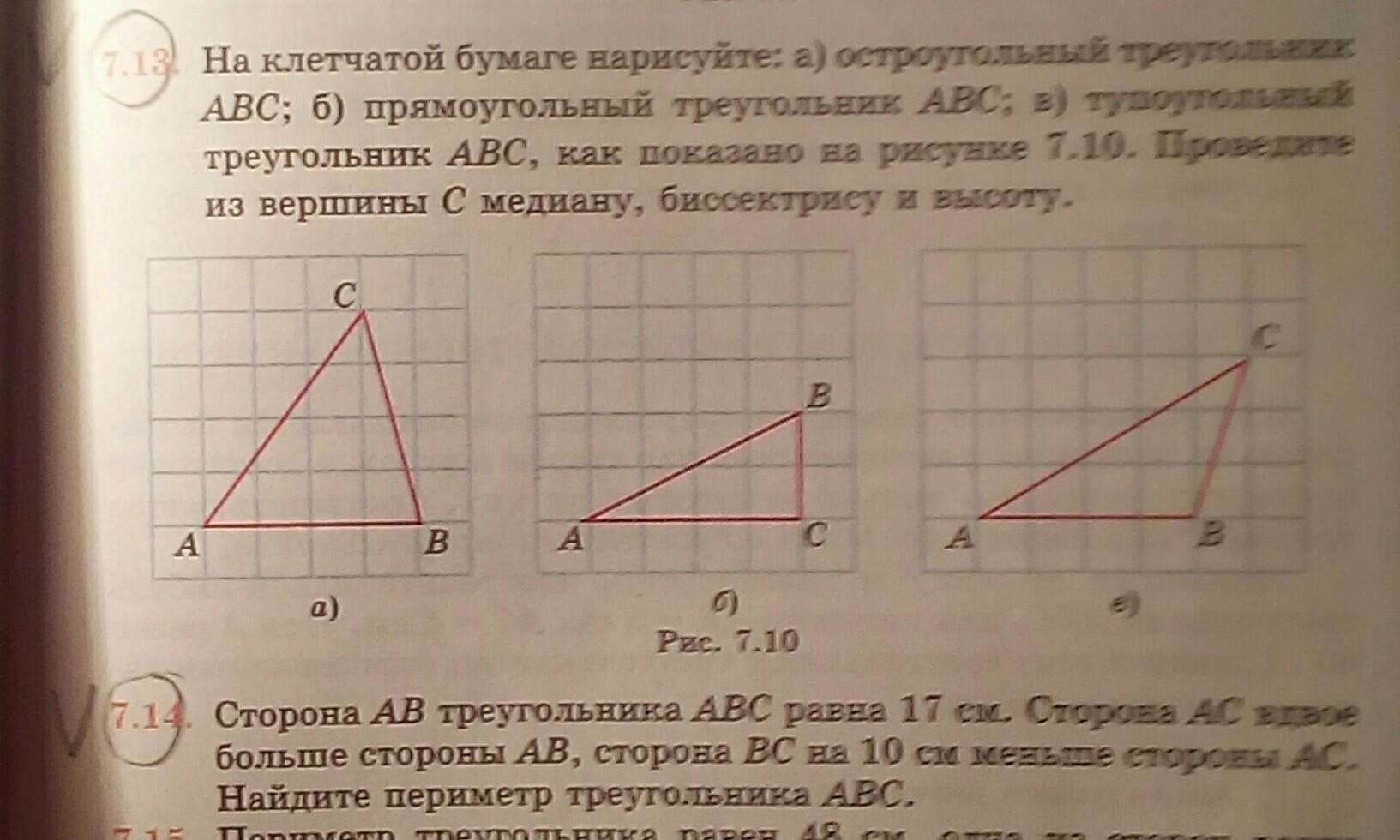
На клетчатой бумаге нарисуйте: а) остроугольный треугольник АВС; б) прямоугольный треугольник АВС; в) тупоугольный треугольник АВС, как показано на рисунке. Постройте из вершины С медиану, биссектрису и высоту.
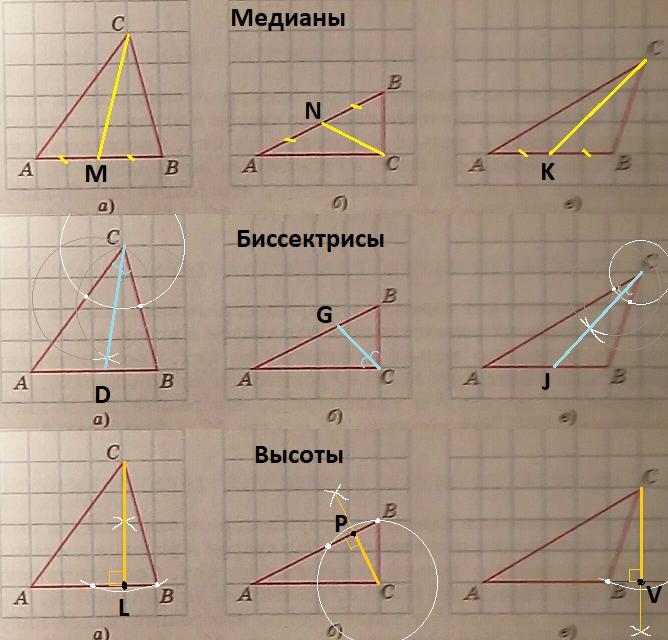
Медиана треугольника - это отрезок, который соединяет вершину с серединой противоположной стороны.
а) Длина отрезка АВ составляет 4 клетки. Середина отрезка точка M поделит его на две части по 2 клетки. Медиана CM.
б) Отрезок АВ по вертикали занимает 2 клетки. Точка N поделит отрезок по вертикали на части по одной клетке. По теореме Фалеса точка N делит отрезок АВ пополам. Медиана CN.
в) Длина отрезка АВ составляет 4 клетки. Середина отрезка K поделит его на две части по 2 клетки. Медиана CK.
==========================================
Биссектриса треугольника - это отрезок биссектрисы угла, расположенный внутри треугольника. Биссектриса делит угол пополам.
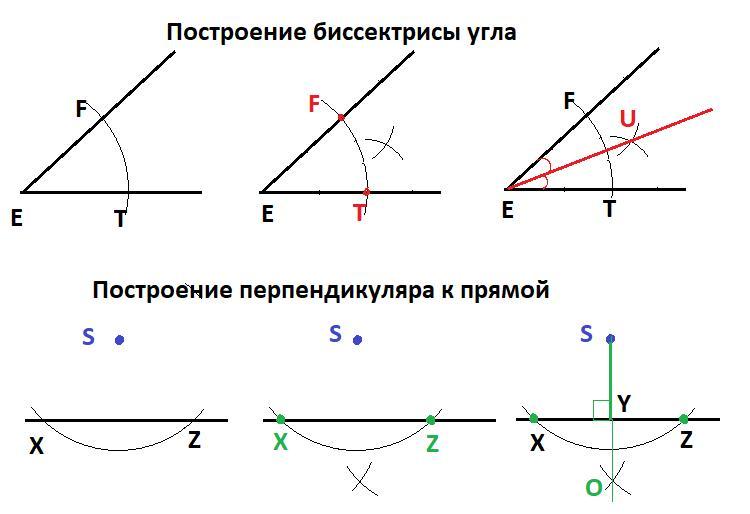
Построение биссектрисы угла во втором приложении.
1) Из вершины угла E произвольным радиусом построить дугу, пересекающую стороны угла. Точки F и T.
2) Из точек F и T одинаковым радиусом построить две дуги, чтобы они пересеклись. Точка U.
3) Построить луч EU. EU - биссектриса угла FET.
---------------------------------------------------------------------
а) CD - биссектриса угла ACB.
б) Так как угол С прямой, то биссектрису можно построить как диагональ маленького квадрата клетки. CG - биссектриса угла ACB.
в) CJ - биссектриса угла ACB
===========================================
Высота треугольника - это перпендикуляр, опущенный из вершины к прямой, содержащей противоположную сторону треугольника.
Построение перпендикуляра из заданной точки к прямой во втором приложении.
1) Из заданной точки S произвольным радиусом провести дугу, пересекающую прямую в двух точках X и Z.
2) Из точек X и Z одинаковым радиусом построить две дуги, чтобы они пересеклись. Точка O.
3) Построить прямую SO. SO⊥XZ. SY - перпендикуляр к прямой XZ.
------------------------------------------------------------------
а) CL - высота треугольника ABC
б) CP - высота треугольника ABC
в) CV - высота треугольника ABC, проведена к продолжению стороны AB и расположена вне треугольника, так как угол B тупой.