Предмет: Алгебра,
автор: Аноним
Алгебра 10 класс
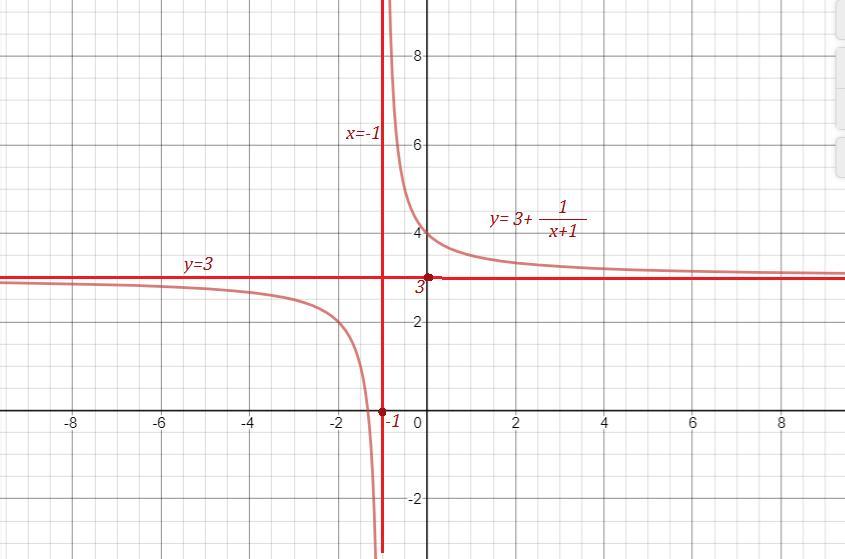
2 задание
Только начертить пожалуйста
Приложения:
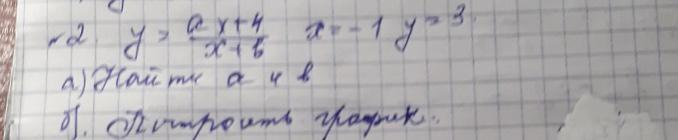
NNNLLL54:
что такое х=1 и у=3 ???
Ответы
Автор ответа:
1
или
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Irikhi
Предмет: Русский язык,
автор: Irrrrrraa
Предмет: Русский язык,
автор: LeriaCat
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Barkan