Предмет: Геометрия,
автор: dashatytyast
Побудуйте переріз правильного тетраедра площиною, що проходить через
бісектрису грані і протилежну цій грані вершину. Обчисліть площу утвореного
перерізу, якщо ребро тетраедра дорівнює 5 см.
Ответы
Автор ответа:
7
Грани правильного тетраэдра - равносторонние треугольники.
Их биссектриса является и высотой и медианой.
В сечении образуется равнобедренный треугольник, одна сторона которого равна ребру тетраэдра, две других - высоты грани.
Высота грани h = a*cos 30° = a√3/2 = 5√3/2.
Площадь сечения можно определить или 1) по формуле Герона, или 2) через высоту сечения.
1) Полупериметр p = 6,83013. Площадь S = √(p(p-a)(p-b)(p-c).
Поставив данные, получаем:
S = √( 6,83013*1,830123*2,5*2,5) = √78,125 = 8,83883.
2) Высота сечения из середины ребра на противоположное ребро равна:
h(c) = √(h² - (a/2)²) = √(18,75 - 6,25) = √12,5 ≈ 4,33013.
S = (1/2)*h(c)*a = (1/2)*5*4,330135 = 8,83883.
Приложения:
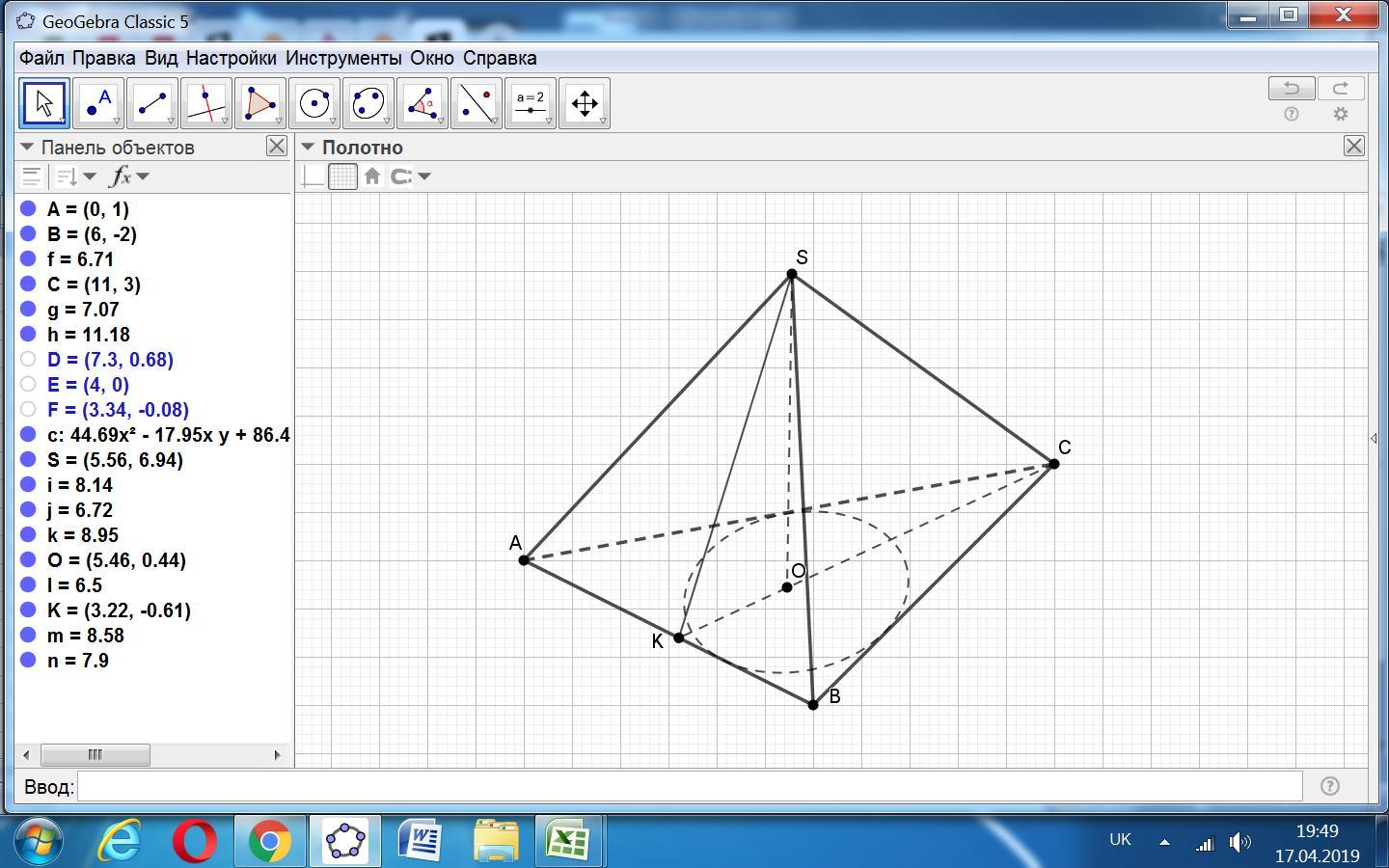
Похожие вопросы
Предмет: Русский язык,
автор: nastyu10
Предмет: Русский язык,
автор: fesenko198494
Предмет: Математика,
автор: Незнайкаеее
Предмет: Алгебра,
автор: reginamukhamet