Предмет: Геометрия,
автор: cobakacytylaj
Вычислить модуль тангенса угла при вершине равнобедренного треугольника с наибольшей площадью, при условии, что дана длина медианы, проведенной к боковой стороне данного треугольника. Записать ответ с точностью до сотых.
Ответы
Автор ответа:
1
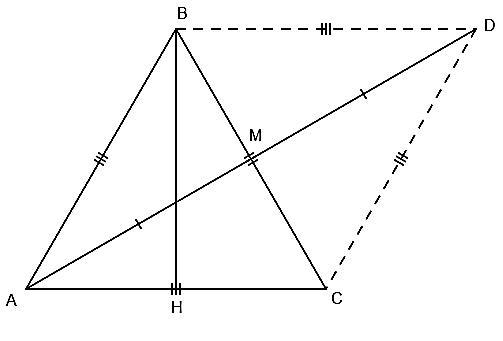
Обозначим медиану AM = a, где a — постоянное число.
Пусть и
.
Достроим до параллелограмма , тогда по теореме: Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон
Далее проведём высоту к стороне основания
. Согласно теореме Пифагора
.
Будем рассматривать следующую функцию площади тр-ка:
Под корнем выражение можно выделить в полный квадрат.
Причем функция принимает наибольшее значение при условии
откуда
и её значение равно
.
, то есть
и все углы по 60°, значит это равносторонний треугольник и тогда искомое значение
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: zorgon
Предмет: Русский язык,
автор: riha1722
Предмет: Английский язык,
автор: volodya0727
Предмет: Литература,
автор: ЕленаИгнатьева