Предмет: Алгебра,
автор: Аноним
упростите выражения 7 класс сор 1 вариант( дроб сверху n-5снизу 2m-3 * 8n m3
Ответы
Автор ответа:
5
Ответ:
Объяснение:
Оригинал задачи в приложении.
Упростите выражение:
Нужно знать:
Решение.
Приложения:
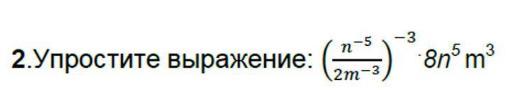
Похожие вопросы
Предмет: Английский язык,
автор: nikas836
Предмет: Українська мова,
автор: linaishchenko
Предмет: Русский язык,
автор: kosarev29102006
Предмет: Математика,
автор: MrCrack1
Предмет: Биология,
автор: AlVi111