Предмет: Алгебра,
автор: petrovichsugar
СРОЧНО, помогите решить с помощью интервалов
Приложения:
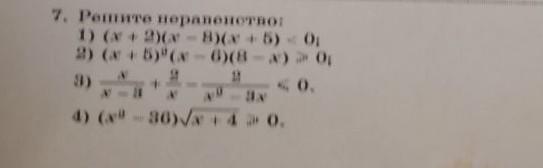
Ответы
Автор ответа:
1
Объяснение:
1) (x+2)(x-8)(x+5)<0
-∞__-__-5__+__-2__-__8__+__+∞
Ответ: x∈(-∞;-5)U(-2;8).
2) (x+5)²(x-6)(8-x)≥0
(х+5)²≥0 ⇒
-∞__-__[-5]__-__6__+__8__-__+∞
Ответ: x∈[-5]U[6;8].
ОДЗ: х≠0 х≠3.
-∞__+__-4__-__0__+__2__-__3__+__+∞ ⇒
Ответ: x∈[-4;0)U[2;3).
4) (x²-36)*√(x+4)≥0
(x+6)*(x-6)*√(x+4)≥0
Так как х+4≥0 x≥-4 ⇒
-4__-__6__+__+∞
Ответ: х∈[6;+∞).
Похожие вопросы
Предмет: Русский язык,
автор: DearEarl
Предмет: Русский язык,
автор: ReginaSheryazova
Предмет: Русский язык,
автор: yanarybnikova
Предмет: Алгебра,
автор: дарья1500
Предмет: Математика,
автор: RahikoGO0