Question

в трапеции основания равны 14 м и 19 м , а боковые стороны 6м и 8м , найти углы трапеции

Answer 1

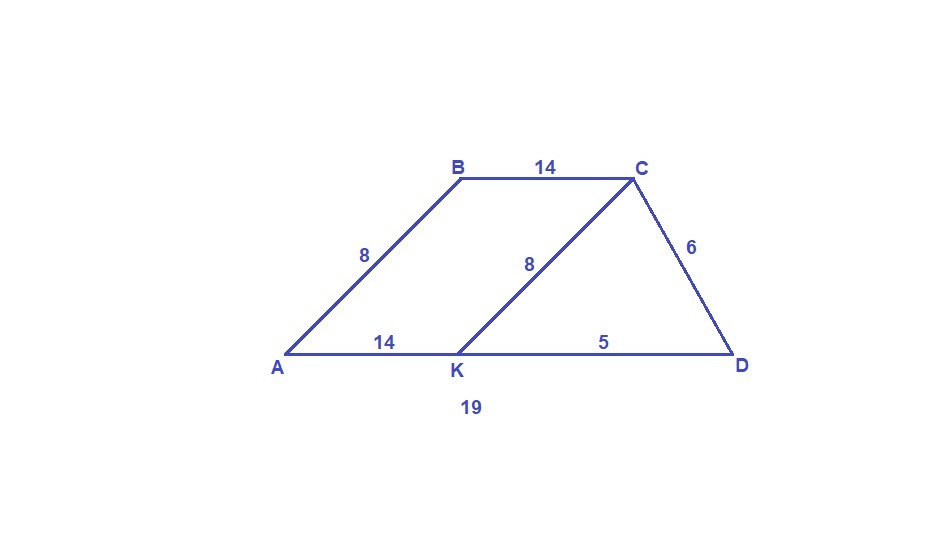
ABCD - трапеция.

Проведем СК║АВ, тогда АВСК - параллелограмм (противоположные стороны параллельны), значит

АК = ВС = 14 м      и      СК = АВ = 8 м

KD = AD - AK = 19 - 14 = 5 м

Из треугольника KCD по теореме косинусов найдем углы К и D:

cos∠D = (CD² + KD² - KC²) / (2 · CD · KD)

cos∠D = (36 + 25 - 64) / (2 · 6 · 5) = - 3 / 60 = - 1/20

∠D = arccos(-1/20) = 180° - arccos(1/20) ≈ 180° - 87° ≈ 93°

cos∠CKD = (CK² + KD² - CD²) / (2 · CK · KD)

cos∠CKD = (64 + 25 - 35) / (2 · 8 · 5) = 54/80 = 27/40

∠CKD = arccos(27/40) ≈ 48°

∠BAD = ∠CKD ≈ 48° как соответственные при пересечении параллельных прямых АВ и СК секущей AD.

Сумма углов трапеции, прилежащих к боковой стороне, равна 180°, поэтому

∠АВС = 180° - ∠BAD ≈ 180° - 48° ≈ 132°

∠BCD = 180° - ∠D ≈ 180° - 93° ≈ 87°