Question

даны прямая и отрезок.Постройте точку ,такую ,чтобы перпендикуляр ,опущенный из этой точки на прямую ,равнялся данному отрезку.

Answer 1

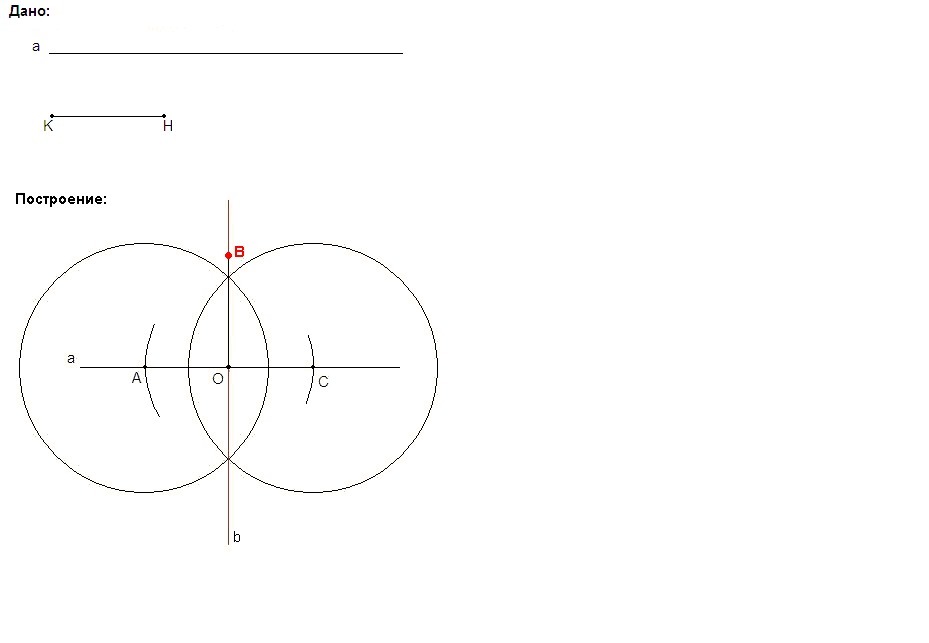
     На прямой а отметим произвольную точку О.
     С центром в точке О проведем окружность произвольного радиуса.    Точки пересечения этой окружности с прямой а назовем А и С.
     С центрами в точках А и С построим две окружности одинакового произвольного радиуса (большего половины отрезка АС).
     Через точки пересечения этих окружностей проведем прямую b. Эта прямая -  серединный перпендикуляр к отрезку АС, значит пройдет через его середину - точку О.
     На прямой b от точки О отложим отрезок ОВ, равный данному КН.
     В - искомая точка.