Предмет: Алгебра,
автор: Grishador02
Решите предел пожалуйста, без правила Лапиталя...
Приложения:
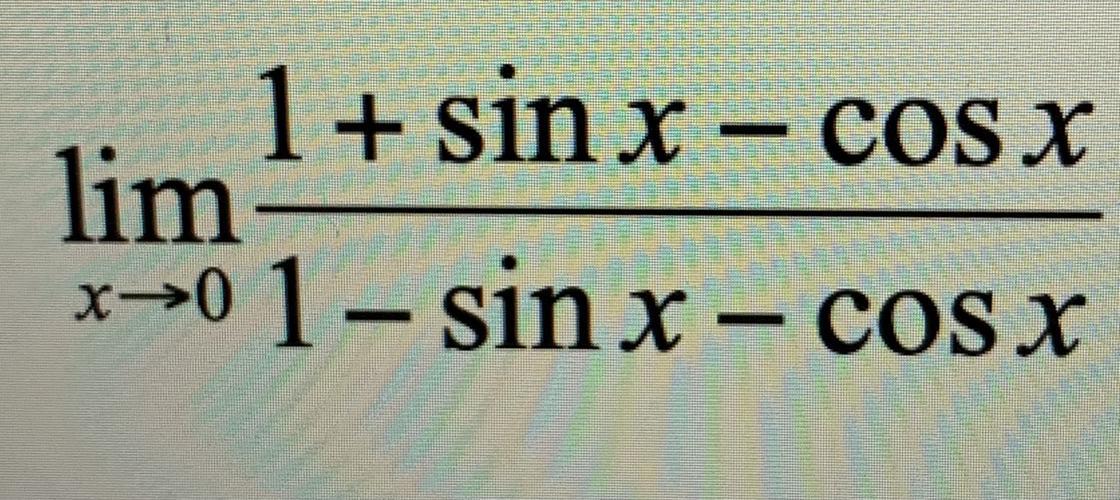
Ответы
Автор ответа:
1
Grishador02:
Спасибо большое!!!!
Похожие вопросы
Предмет: Русский язык,
автор: 200208
Предмет: Английский язык,
автор: Makskoldj
Предмет: Русский язык,
автор: dimafursov
Предмет: Математика,
автор: zairbek05ru05