Предмет: Геометрия,
автор: marta2635
127. Дано дABC з вершинами A(-2; 5), B(6; 3), C(4; -3). Знайдіть довжини середніх ліній трикутника.
Приложения:

Ответы
Автор ответа:
10
Ответ:
ДК=5, КЕ=√17, ЕД=√10
Объяснение:
обозначим точки середин сторон ∆АВС: Д К Е, при этом Д лежит на стороне АВ, К - на стороне ВС, Е - на АС. Получился ∆ДКЕ. Вычислим координаты каждой точки Д К Е по формуле вычисления середины отрезка:
Итак: Д(2; 4)
Таким же образом найдём координаты остальных
точек К и Е:
Итак: К (5; 0)
Итак: Д(2; 4), К(5; 0) Е (1; 1)
Теперь найдём длины сторон ДК, КЕ, ЕД по формуле: ДК²=(Дх–Кх)²+(Ду–Ку)²=
=(2–5)²+(4–0)²=(–3)²+4²=9+16=25;. ДК=√25=5
КЕ²=(5–1)²+(0–1)²=4²+(–1)²=16+1=17; КЕ=√17
ЕД²=(2–1)²+(4–1)²=1²+3²=1+9=10; ЕД=√10
Приложения:
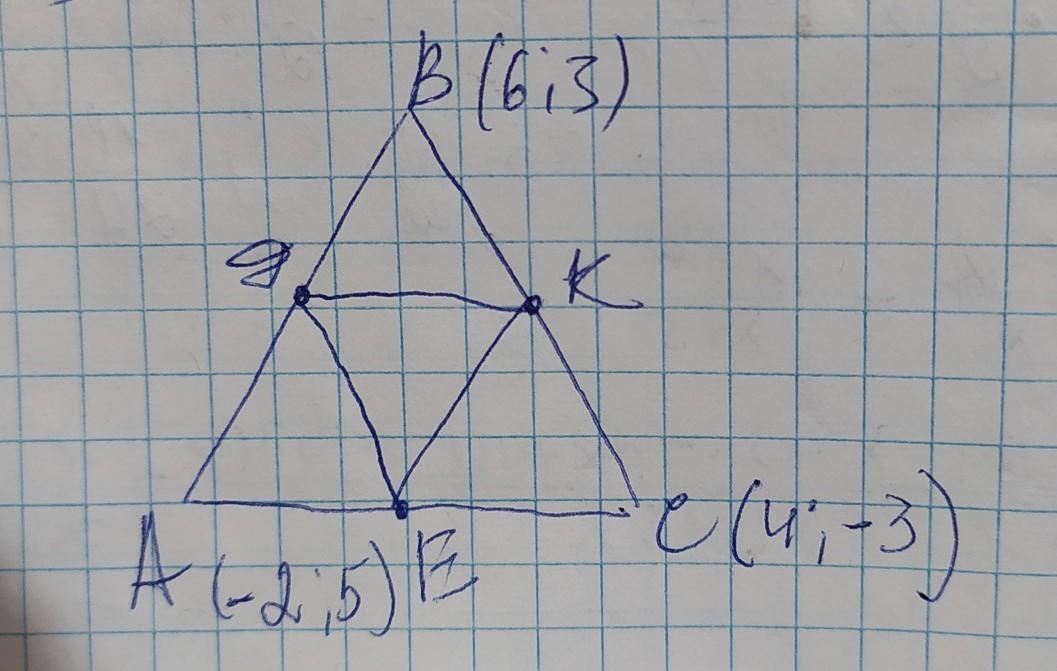
marta2635:
дякую!!!
будь ласка))
Похожие вопросы
Предмет: Русский язык,
автор: ruzil461
Предмет: Английский язык,
автор: dianaamaeva23
Предмет: Українська мова,
автор: Yanka0Z0
Предмет: Литература,
автор: alexakalimulli
Предмет: Литература,
автор: DashaTrue153