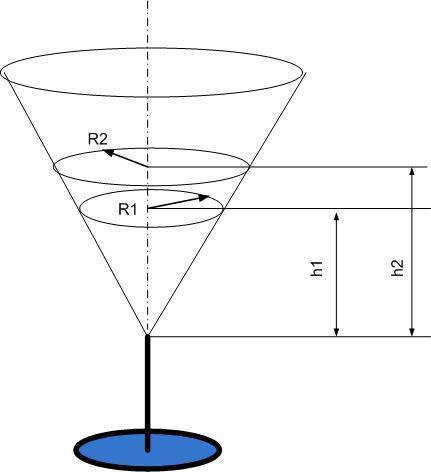
бокал имеет форму конуса. в него налита вода на высоту равную 4. если в бокал долить воды объемом равный одной четвертой объема налитой воды, то вода окажется на высоте равной:
помогите пожалуйста очень срочно нужно.
Ответы
Ответ:
h₂=2∛10≈4.31
Пошаговое объяснение:
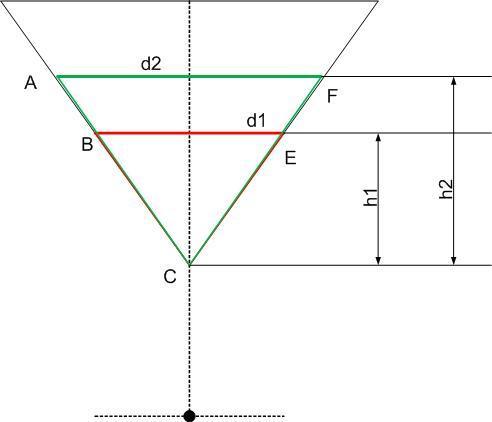
рассмотрим рис. "сечение бокала". Здесь нарисованы осевые сечения бокала-конуса плоскостью для объемов V₁ и V₂ (проходящей через центр окружности-основания конуса, и перпендикулярной этому основанию):
Δ BCE - сечение для объема V₁ (высота воды - h₁ диаметр d₁ или радиус r₁)
Δ CAF - сечение для объема V₂ (высота воды - h₂ диаметр d₂ или радиус r₂).
Эти треугольники подобные по признаку равенства двух соответствующих углов обоих треугольников, следовательно и оба наших конуса-объема - подобные тела.
Для подобных тел можем записать:
h₂=kh₁ и r₂=kr₁ (1)
объем первого конуса: V₁=(h₁*πr₁²)/3;
объем второго конуса: V₂=(h₂*πr₂²)/3;
или с учетом (1): V₂=k*h₁*π*(k*r₁)²=k³*(h₁*π*r₁²)=k³*V₁;
окончательно: V₂/V₁=k³; k=h₂/h₁; V₂/V₁=(h₂/h₁)³; h₂=h₁∛(V₂/V₁).
Подставим числовые значения в нашу формулу:
по условию: V₂=V₁+V₁/4=5V₁/4;
V₂/V₁=5V₁/(4V₁)=5/4;
h₂=h₁∛(V₂/V₁)
с учетом, что h₁=4 получим: h₂=4∛(5/4)=∛(4³*5)/4)=∛(16*5)=∛(8*10)=2∛10≈4.31