Question

Квадратная таблица 3×3 заполнена попарно различными цифрами таким образом, что все трехзначные числа, которые можно прочитать в строках этой таблицы слева направо и в столбцах сверху вниз, делятся на 6. Сколько из этих шести чисел могут делиться на 5? Перечислите все возможности и докажите, что других возможностей нет.СРОЧНО!!! ДАЮ 50 БАЛЛОВ

Answer 1

Ответ: Только одно число кратное $5$, других вариантов быть не может.

Пошаговое объяснение:

Поскольку все числа слева направо и сверху вниз делятся на $6$, то они являются четными, а значит кончаются на четную цифру. То есть все $5$ цифр находящихся в третьем ряду (сверху) или третьем столбце (справа) являются четными. А поскольку среди цифр от $0$ до $9$ , четных как раз ровно пять: $0;2;4;6;8$ , то все данные цифры висят в третьем ряду или третьем столбце.  Число делиться на 5, когда оно кончается на 0 или 5, но цифра 5 нам не подходит, ибо является нечетной. Поэтому число кратное 5 кончается на 0.

Если цифра $0$ находиться в правом нижнем углу, то возможно два числа кратных $5$, в иных же случаях может быть не более одного числа кратного пяти, поскольку цифра 0 является пересечением ровной одной строки и одного столбца.

Рассмотрим случай, когда $0$ находится в правом нижнем углу.

Поскольку число кратно $6$, то оно кратно и $3$, а значит сумма цифр делиться на 3. При данной конфигурации цифра 0 является пересечением третьей строки и третьего столбца, а значит сумма всех остальных четных чисел кратна 3, однако :

$2+4+6+8=20$, что не делиться на 3.

Таким образом, данный случай невозможен.

Рассмотрим теперь случай, когда число кратное $5$, единственное.

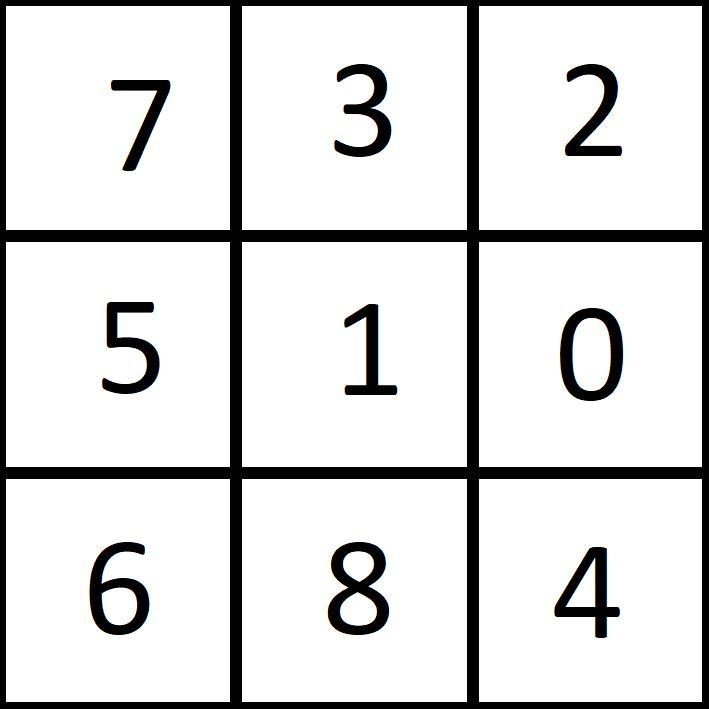
В силу симметрии таблицы выберем произвольно, что $0$ будет находиться во второй строке и третьем столбце.  Добиться нужного расположения чисел в данном случае достаточно легко, используя, что сумма цифр делиться на $3$. (Смотрите рисунок $1$)

Все трехзначные числа сверху вниз и слева направо делятся на $6$.

Добиться того, чтобы ни одно из чисел не делилось на $5$ невозможно, поскольку $0$ стоит в одном из мест третьего столбца или третьей строки.