Предмет: Математика,
автор: 4hdxsizi5n
В треугольнике ABC угол C=90’, AC=1, BC=√90. Найдите cos A
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Дано:
Найти:
cos A = ?
Решение
Т.к. угол С = 90°, треугольник АВС прямоугольный, с гипотенузой АВ.
А значит косинус угла А будет равен отношению прилежащего к углу катета АС к гипотенузе АВ
По Т. Пифагора
Приложения:
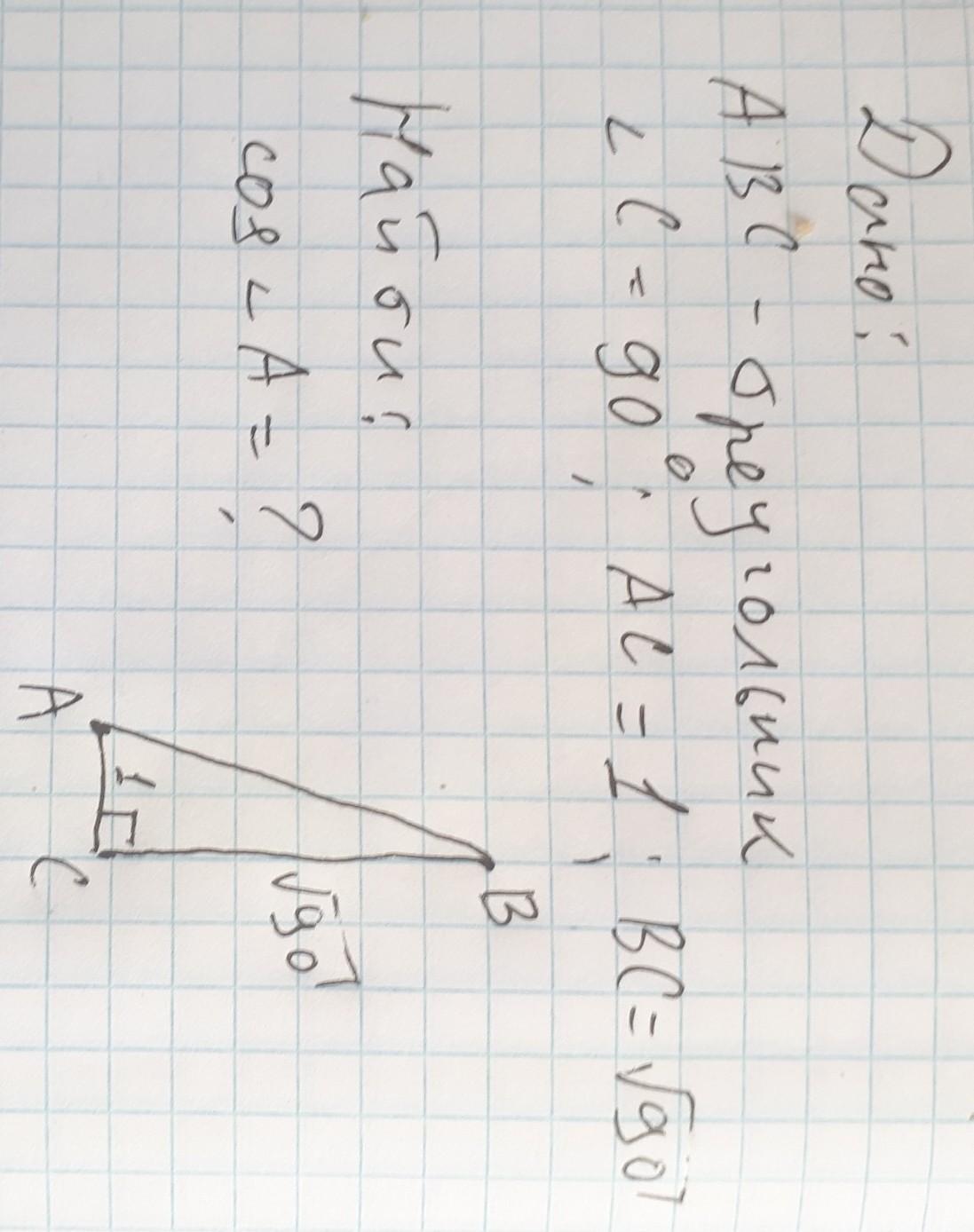
Похожие вопросы
Предмет: Русский язык,
автор: Маша0070
Предмет: Русский язык,
автор: 5yanayana
Предмет: Русский язык,
автор: kuksa403
Предмет: Геометрия,
автор: AlinkaHund2216