Question

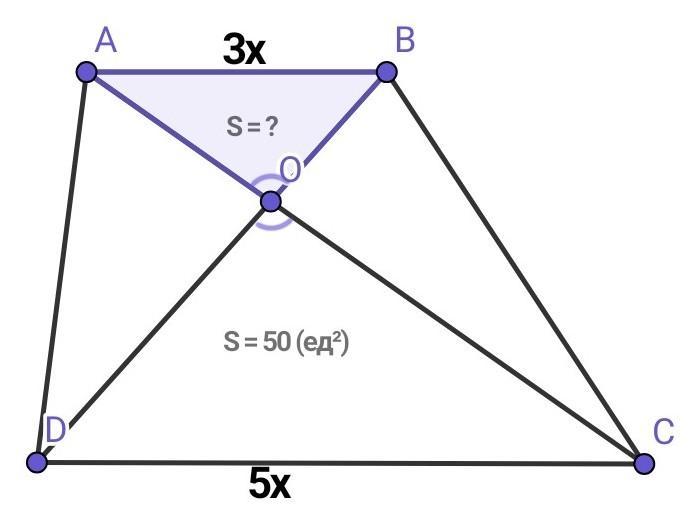
в трапеции abcd,(ab||cd) отношение оснований равно 3:5 и диагонали пересекаются в точке o. найдите площадь треугольника aob, если площадь треугольника cod=50

Answer 1

Дано :

Четырёхугольник ABCD — трапеция (AB || CD).

AB : CD = 3 : 5.

Отрезки BD и AC — диагонали.

Точка О — точка пересечения диагоналей.

S(∆COD) = 50 (ед²).

Найти :

S(∆AOB) = ?

Решение :

• Диагонали трапеции, пересекаясь, образовывают два подобных треугольника (подобны только те, одни из сторон которые являются основания трапеции).

Отсюда —

∆DOC ~ ∆ВОА.

<DOC = <BOA (как вертикальные).

Тогда AB и CD — сходственные стороны (по определению).

• Отношение сходственных сторон подобных треугольников равно коэффициенту подобия.

Пусть AB = 3x, тогда CD = 5x (по условию задачи).

Тогда —

k = AB/CD = 3x/5x = 3/5 = 0,6.

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Отсюда —

S(∆BOA)/S(∆DOC) = k² (здесь главное написать всё в том порядке, в котором мы делали. То есть, ища коэффициент подобия, мы ставили в числитель меньший треугольник, так и здесь : в числитель ставим меньший треугольник).

S(∆BOA)/50 (ед²) = 0,6²

S(∆BOA)/50 (ед²) = 0,36

S(∆BOA) = 18 (ед²).

Ответ :

18 (ед²).