Предмет: Математика,
автор: OsirisOsiris
Решите, пожалуйста, два предела, с помощью замены, без использования правила Лопиталя....спасибо заранее
Приложения:
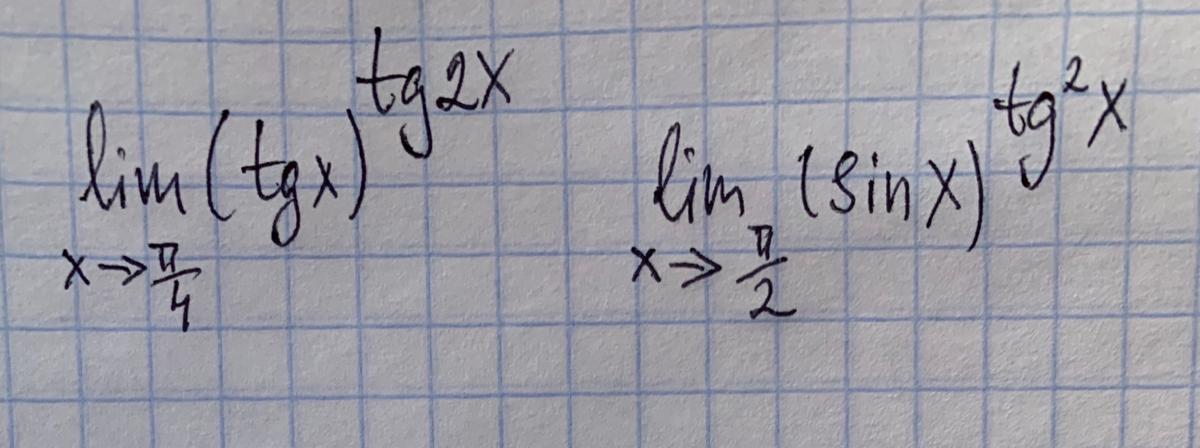
Ответы
Автор ответа:
1
Обозначим:
Логарифмируем:
Знак предела и знак непрерывной функции можно менять местами:
Применяем свойство логарифма степени
Запишем в виде дроби:
неопределенность (0\0)= ( проще по правилу Лопиталя):
Значит,
OsirisOsiris:
Спасибо, хоть кто-то! У меня что-то пошло не так, получилось просто e^1/4 в первом)
Похожие вопросы
Предмет: Українська мова,
автор: 380989441086
Предмет: Русский язык,
автор: kutuzjo777
Предмет: Русский язык,
автор: kamila16121982
Предмет: Математика,
автор: flashyspring194
Предмет: Литература,
автор: mishaterentev