Question

Відношення гострих кутів прямокутного трикутника 8:7. Знайдіть кут між бісектрисою і висотою, які проведені з вершини прямого кута.
(з поясненням) ​

Answer 1

Отношение острых углов прямоугольного треугольника 8: 7. Найдите угол между биссектрисой и высотой, которые проведены с вершины прямого угла.

Объяснение:

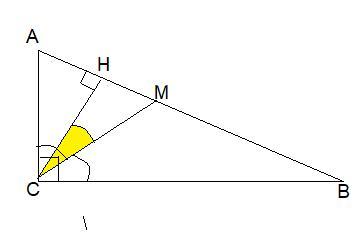
Углом между биссектрисой и высотой будет ∠МСН.

Пусть одна часть х° , тогда ∠А=8х , ∠В=7х.

∠А+∠В=90° ,   15х=90° , х=6°    ⇒  ∠А=48°  ,  ∠В=42°.

ΔСМВ, ∠МСВ=45° т.к. СМ-биссектриса  , ∠МВС=42° ⇒

∠СМВ=180°-(45°+42°)=93°.

ΔМСН-прямоугольный, ∠СМВ для него внешний. По т. о внешнем угле ∠СМВ=∠МСН+∠СНМ ,

93°=90°+∠МСН ,

∠МСН=3° .