Предмет: Геометрия,
автор: AppleGameplays5
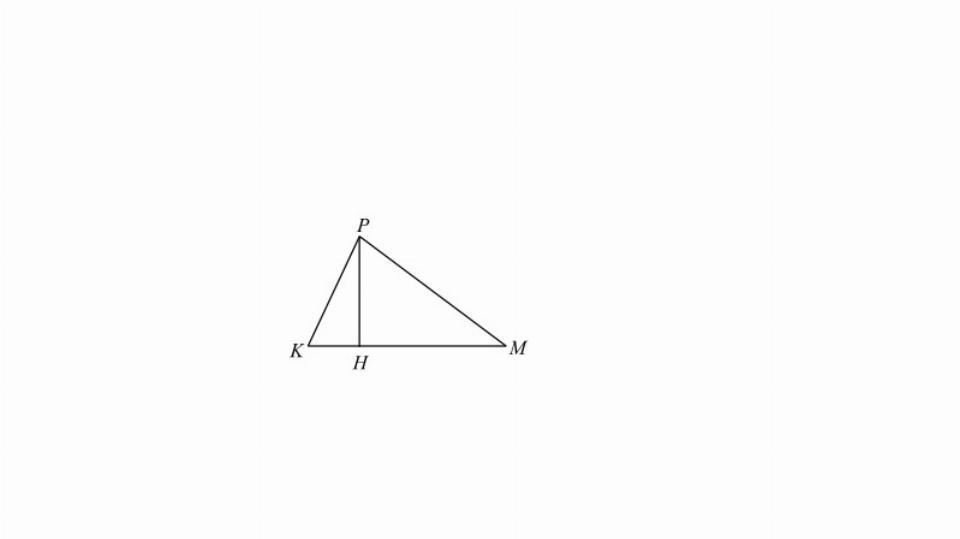
В остроугольном треугольнике MPK высота PH равна  , а сторона PM равна 50. Найдите cos M
, а сторона PM равна 50. Найдите cos M
Приложения:
Ответы
Автор ответа:
0
Рассмотрим прямоугольный треугольник АНМ. В нем
РН/РМ=sinМ=(5√51)/50=√51/10; cosМ=√(1-sin²М)=√(1-51/100)=
√(49/100)=0.7
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: неизвестна
Предмет: Русский язык,
автор: Grandera
Предмет: Английский язык,
автор: dominikablak
Предмет: Геометрия,
автор: Mixail3241