Предмет: Математика,
автор: supernat83
При каком наименьшем натуральном “a” уравнение имеет решение.
Приложения:
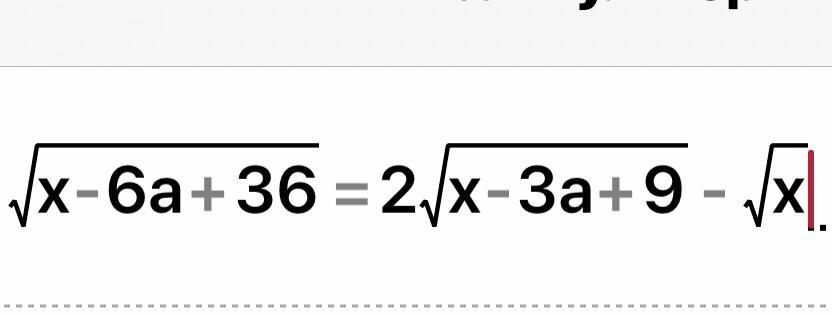
zzyto1:
где-то да, где-то нет
что значит как определять? есть четкое определение натуральных чисел, где сказано, что натуральное число начинается с 1
в вики написано, что можно и так и так.
вики-это последний сайт, которому можно доверять
хорошо, тогда при a = 1.
кстати, а почему вики - последний сайт ?
хотя бы потому, что любой человек может туда зайти и отредактировать статью
при желании можно углубиться в источники, там они прилагаются.
ответ: а=12
можете скинуть решение ? у меня на бумаге получился ответ - '6', вероятно ошибка есть.
Ответы
Автор ответа:
2
Ответ:12
Пошаговое объяснение:
Заметим, что условие (2) строже условия (1), а условие (3) выполняется при любых a
Найдем при каких a верно (2) и (4):
Таким образом
Похожие вопросы
Предмет: Русский язык,
автор: marusdiana12
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Rhebp12
Предмет: Алгебра,
автор: Aleksei451