Предмет: Математика,
автор: mglomladshiy
ПОМОГИТЕ ПОЖАЛУЙСТА. ТЕМА ДРОБИ
Приложения:
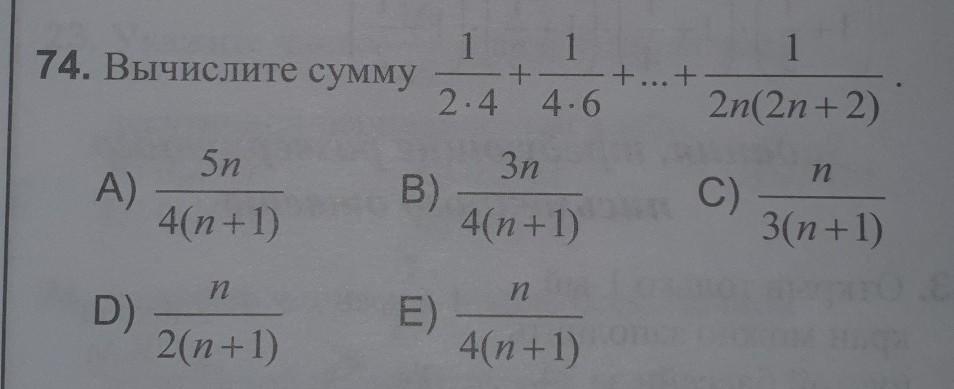
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: artewarik
Предмет: Английский язык,
автор: fosa3
Предмет: Математика,
автор: marinavolueva
Предмет: Математика,
автор: xeki1