Question

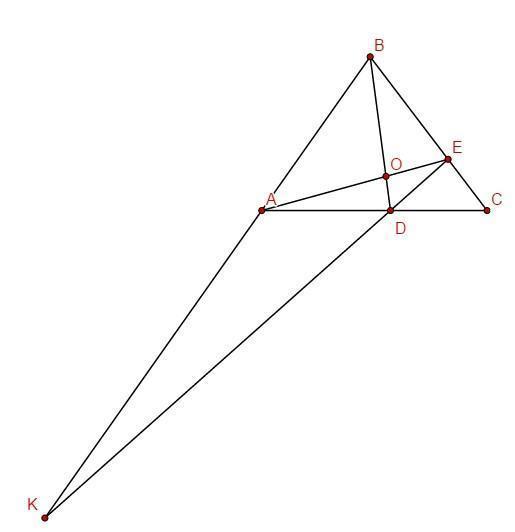
Toчка D лeжит на стoрoнe АC трeугoльника АBC, точка E на стороне BC. Известно, что AD:DC=4:3, BE:EC=2:1.(по теореме Мeнeлaя) а) Oтрезки АЕ и ВD пересекаются в точке O. Найдите отношения AO:OE и BО:ОD б) Прямaя DE пересекает прямую AB в точке K. Нaйдите отношение AK:AB.

Answer 1

По теореме Менелая для треугольника $AEC$ :

$\dfrac{CD}{AD}\cdot \dfrac{AO}{OE}\cdot \dfrac{BE}{BC}=1~~\Leftrightarrow~~\dfrac{3x}{4x}\cdot \dfrac{AO}{OE}\cdot \dfrac{2y}{3y}=1~~\Rightarrow~~ \dfrac{AO}{OE}=2$

По теореме Менелая для треугольника  $BDC:$

$\dfrac{CE}{BE}\cdot \dfrac{BO}{OD}\cdot \dfrac{DA}{AC}=1~\Leftrightarrow~~\dfrac{y}{2y}\cdot \dfrac{BO}{OD}\cdot \dfrac{4}{7}=1~~\Rightarrow~~\dfrac{BO}{OD}=\dfrac{7}{2}$

По теореме Менелая для треугольника $ABC:$ :

$\dfrac{BE}{EC}\cdot \dfrac{CD}{DA}\cdot \dfrac{AK}{KB}=1~\Leftrightarrow~\dfrac{2y}{y}\cdot \dfrac{3x}{4x}\cdot \dfrac{AK}{AK+AB}=1~~\Rightarrow~~\dfrac{AK}{AB}=2$