Предмет: Геометрия,
автор: vfdsrukhf
ПОМОГИТЕ ПОЖАЛУЙСТА РАЗОБРАТЬСЯ 35 БАЛЛОВ
Докажите что площадь четырехугольника abcd равна

Приложения:
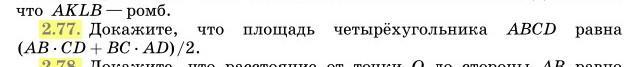
vfdsrukhf:
теперь понятно
а как доказать что вписанного четырехугольника диагонали пересекаются в 90°
в задании не указано, что четырехугольник вписанный...
ну как сказать...
как так в книге есть такие задачи что 10-20 задач вопросы разные но условие тоже самое
тут тоже самое в первые даёт условия и потом в вопросах не пишет
я не знаю что у вас за книга, но у вас фото задачи, в которой нет ни слова о вписанном четырехугольнике
значит в решении это надо учитывать
если хотите я вам скину фото как выглядит 7-8 задачах в одном условием
В этом параграфе ABCD-вписанный четырёхугольник, диагонали которого перпендикулярны. Мы будем использовать также следующие обозначения: О-центр описанной окружности четырехугольника ABCD, P- точка пересечения диагоналей.
Ответы
Автор ответа:
2
Раз четырехугольник вписан в окружность, воспользуемся теоремой Птолемея. т.е. произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Диагонали у четырехугольника равны АС и ВD, а сумма произведений противолежащих сторон АВ*СD+ВС*АD, из которого следует
АС*ВD/2=(АВ*СD+ВС*АD)/2, левая часть равенства - известная формула площади четырехугольника с взаимно перпендикулярными диагоналями.
Доказано.
Похожие вопросы
Предмет: Русский язык,
автор: lili1984
Предмет: Русский язык,
автор: daryamadalieva
Предмет: Русский язык,
автор: Loginov20021
Предмет: Математика,
автор: NeI3VeSntiY