Предмет: Алгебра,
автор: happy123456
Помогите пожалуйста решить уравнение
Приложения:
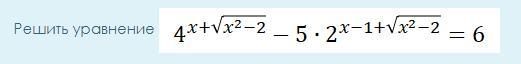
Ответы
Автор ответа:
1
...................................
Приложения:

Автор ответа:
1
Пусть = t :
Обратная замена :
1)
Возведем обе части уравнения в квадрат, при условии что правая часть уравнения ≥ 0 :
2 - x ≥ 0
x ≤ 2
-------------
- ответ
1.5 меньше 2, то есть корень нам подходит.
2)
x ∈ ∅
Ответ : x = 1.5
Похожие вопросы
Предмет: Русский язык,
автор: 2002Evgenia2002
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: nadin2201kiss
Предмет: Математика,
автор: габыч
Предмет: Литература,
автор: давид278